lmbrls, post: 381655, member: 6823 wrote: I just give the curve Length, Arc Distance, Radius, Chord Bearing and Distance. ...
Oregon law requires that those 5 elements be shown on plats. Perhaps for that reason it is common around here to include them all in descriptions.
[INDENT=1]... [Bearing], [Distance] to the beginning of a xx.xx foot radius curve to the right(left); THENCE along said curve xx.xx feet through a central angle of xxå¡ xx' xx" (the chord of said curve bears [Bearing], [Distance]); THENCE [Bearing], [Distance] ...[/INDENT]
Wattles states that tangency is assumed and it is only necessary to specify when a curve is non-tangent. That's how I roll.
That is how I roll too. It is tangent unless stated otherwise.
I agree with the need for central angles and accuracy. When done correctly, it can make a complicated description easy to compute. I have adopted the method described by Gurden H. Wattles in his text Writing Legal Descriptions, the one with the yellow cover and blue text. Here is a recent sample of some intersecting curves.
Ken
thence along said division line, North 42å¼ 02' 40" West 535.85 feet to the intersection of a 125.00 foot radius curve in the east right of way line of said [road], to which intersection a radial line bears North 23å¼ 38Ûª 00Û West;
thence northeasterly along the division line between said [road] and Lot 7, with the arc of said 125.00 foot curve, deflecting to the right through a central angle of 21å¼ 49' 50" an arc distance of 47.63 feet to the intersection of a 65.00 foot radius curve, to which intersection a radial line bears South 65å¼ 34Ûª 40Û West;
thence easterly, northerly and westerly along the division line between said [road] and Lot 7 and Lot 6 on said Map No. [xxxx], with the arc of said 65.00 foot curve, deflecting to the left through a central angle of 222å¼ 04' 36" an arc distance of 251.94 feet to the Point of Beginning.
I include delta in all calls, tangent or not, required or not (frankly haven't even looked into whether it is required, just always have taken for granted, i guess, that it's a necessary element to define a curve), and also have an additional subtle variation in language when approaching one in a call:
(tangent): "to the point of curvature of a curve to the left, having a radius of xxx.xx feet, a central angle of xxxx, etc."
(non-tangent): "to the beginning of a non-tangent curve to the left, having..."
It is tangent if the line is tangent to the curve. It is non-tangent if the line is non-tangent with the curve.
As for how to describe the boundary, we are supposed to be professionals - figure it out. If you can't figure it out, please stick to pounding hubs.
We certainly don't (or at least we shouldn't) need laws to tell us how to write descriptions.
Continuing the hijack of this thread...
I used to describe curves much like Kevin describes, until I came across this one.
At the center of the 22 foot curve is a well that belongs with the tract to the east. Without the well, the tract to the east is not worth much.
He describes it as beginning at the NW corner of Section 23, thence S 89å¡56'40" E along the north line of said Section 23, 624.68 feet; thence S 00å¡42'20" E, 229.34 feet; thence 69.12 feet along a curve to the right of a radius of 22.0 feet, a central angle of 180å¡00'00", whose radius point bears S 00å¡42'20" E; thence...
The boundary goes around the well to the right, but the arc curves to the left. And the radial bearing doesn't help.
Of course the deed doesn't show the picture. And the survey wasn't recorded. Finally found a copy of the survey and got it straightened out, and now I add "concave easterly" or some such description. 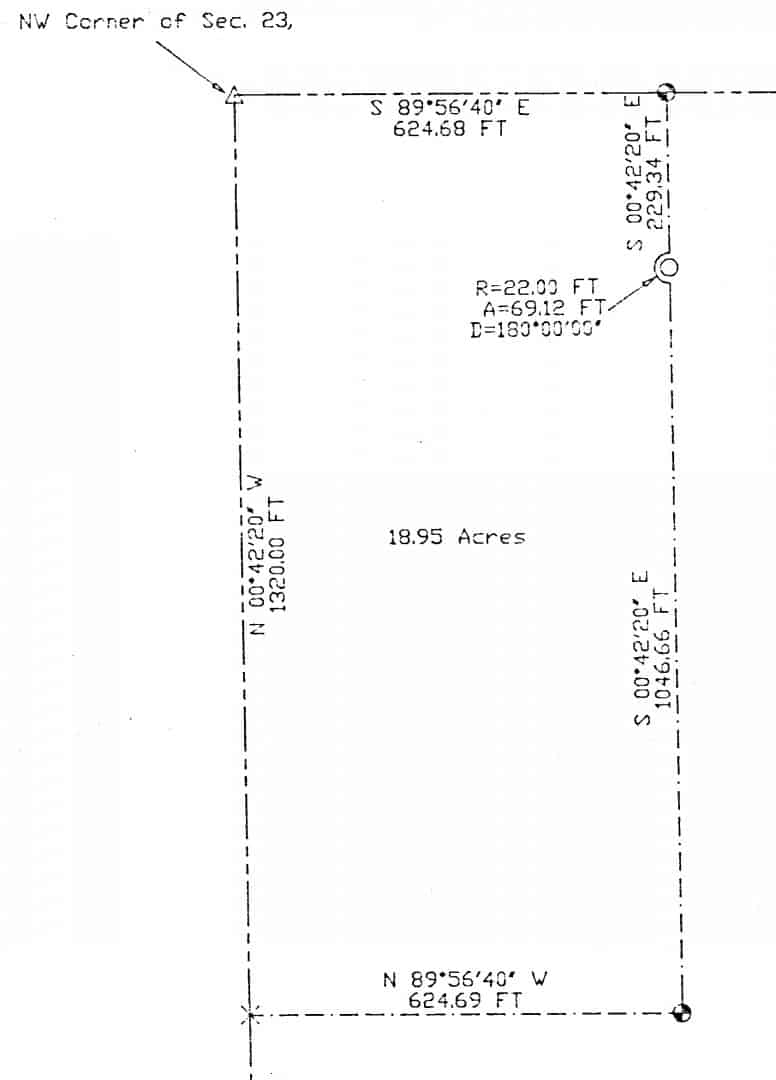
So if I don't give you the delta, you are going to sweat the difference that results from the chord distance being rounded to 0.01' on a property survey? I understand that if you are required to give the delta that you do not want to mathematically conflict with other elements of the curve. However, I can't get very worked up over less than 0.01 of a foot. I think adjusting tribrachs and prism rods will have a much greater practical affect on accuracy. Often, I am accused of picking the fly specks out of the pepper, but this seem microscopic.
The precision of your coordinate geometry calculations and legal descriptions is something you have control over. Why introduce unnecessary errors by using the lesser precise elements to perform the calculations or define the geometry for someone else to calculate in the future? I have seen map checkers bounce subdivision calcs because they did not match the map by even a second on the delta. I have many times seen them squawk when the sum of the total lot frontages does not equal the total tangent length along the centerline/RW by even a hundredth because of rounding error accumulation. Of course I am not going to have heartache over 0.01' between record and measured, or in a lot of other situations, but I am also not going to knowingly introduce rounding errors into legal descriptions or other calculations unnecessarily. It is simply my chosen preference understanding the math involved. I always include the delta, so I simply avoid the conflict by using the radial bearing (on a non-tangent curve) rather than a chord bearing and distance.
D-Day96, post: 381643, member: 6385 wrote: When you're writing a metes & bounds description that requires a curve description, what do you consider a tangent vs. non-tangent curve?
I don't say one way or the other, in my descriptions. Let the reader figure it out:
Beginning at the Northwest corner of said section 13;
Thence North 90å¡ East, along the north line of said section, a distance of 100.00 feet, to a point of curvature to the right, the radius point of which bears South 0å¡ East, 100.00 feet;
Thence along said curve to the right, through a central angle of 90å¡, an arc distance of 157.08 feet to a point of tangency;
thence....
lmbrls, post: 381663, member: 6823 wrote: Is the delta of a curve required in some states in a description?
[USER=6823]@lmbrls[/USER]
Is there requirements, as to how descriptions are written in your state?
What [USER=1333]@Brian Allen[/USER] said...
Brian Allen, post: 381676, member: 1333 wrote: We certainly don't (or at least we shouldn't) need laws to tell us how to write descriptions.
The term "delta angle" used by some can be frustrating to others. Its use is similar to that for "A-size" paper, which is 8.5 by 11 inches, and for "D-size" cells, 60mm long and 33mm diameter. In all cases, the other has to know the associated parameters. If he or she does not, then it is requisite appropriate research is conducted.
"Delta" is the word used to refer to the Greek letter delta. Its use, especially in mathematics and science, generally indicates a difference or change. Historically, "delta," the Greek letter, has been used to indicate the difference in direction between two tangents. And, in the cases where circular curves are used to transition from one tangent's alignment to another, the angular difference between the two tangents is equal in value to the circular curve's central angle. Thus, when a circular curve is not tangent at both ends, the term "delta angle" may not follow convention.
In such a case, the important value becomes the circular curve's central angle and the angular difference, the so symbolized "delta angle," in lead-in and lead-out tangents becomes less relevant.
When the term "central angle" is used within the context of a circular curve, I believe there is greater conveyance of meaning. It is not too far fetched for someone to envision a piece of pie: it is part of a circle and the central angle is at the point. However, the term "delta angle" does not, unless explained, easily come to other's minds. Sufficient meaning is not conveyed.
The term and value for "central angle" provides a completeness of thought about a circular curve. Again, referring to the piece of pie, people generally can deduce that a circular curve is part of a circle. A circle's fundamental parameter is its radius. The "central angle" tells how much of a part of the circle the curve is. Other parameters including chord, tangent distances, mid-ordinate, etc really don't convey a completeness of thought. In any case, these other parameters may, if needed, be computed when the radius and central angle values are provided.
For the sake of better communications, I prefer the term "central angle."
Other comments:
Instead of "curve to the left (or right) concave to the ....," "deflecting to the right (or left)" may be used. In the cases illustrated by Peter Ehlert, the addition of chord length and direction or radial line direction and distance can clarify.
Generally, when a line is tangent to a circle, it is usually understood that the circle is tangent to the line. However, if one wishes to refine the terminology, it can be stated the curve is osculatory to the line.
Excellent point and differentiation. In a legal description, I use the term central angle to define a curve, such as " along the arc of a curve to the left, having a radius of 400.00 feet, through a central angle of 35 degrees (using the degree symbol), an arc length of 128.29 feet; thence......" On a map, the triangle, or delta symbol is used to represent the central angle of the curve being annotated.
It has been many years since I wrote a legal description, but I have written thousands of them in my almost 30 years of being licensed. My area of practice for the past 13 years has been geodesy and geodetic control surveys. I have enjoyed this discussion and knocking off some rust covered memories.
I really hate it when municipalities tell me how to write descriptions. I especially hate it when municipalities expect you to write descriptions a certain way, keep there top secret expectations to themselves, and then send you a nasty-gram when you do not conform. Recently I had the opportunity to have a description come under question because the municipality could not 'close' my description. There reasoning was that I did not provide chord bearings and distances on my curves. After a lengthy discussion of why chord bearings are not needed on tangent curves (and frankly just add more confusion in my opinion) I asked why they couldn't compute my closure. They said "my software can only calculate closures based on chord bearing and distances" this was shortly followed by my question "what if you change software in the future, will you have new hidden legal description requierements?" This was followed by a lengthy silence, which was then followed by a discussion with her manger which then resulted in my description being promptly recorded and moved through the process.
Begrudgingly i now include chord bearing and distance in every curve I describe in this municipality.
(to the beginning of a tangent curve, concave to the South with a radius of 100.00 feet) You can add non-tangent in lieu of tangent and then specify the radial bearing (hopefully to the radius point)
(thence, tangent to said curve) non-tangent with a radial bearing works too
MLSchumann, post: 381695, member: 471 wrote: Instead of "curve to the left (or right) concave to the ....," "deflecting to the right (or left)" may be used.
I'm not sure that would help in the case I showed above. I will admit that it is a special case.
I learned a new word today. Osculatory. :kissing_heart:
,_ post: 381702, member: 9631 wrote:
I learned a new word today. Osculatory. :kissing_heart:
Cool, yo tambien
http://www.thefreedictionary.com/osculatory



