What Does +/- 1SD Mean In Surveying?

I think you've got it. Assuming the errors in your measurements are random (normally distributed), and not systematic, 1, 2, & 3 will all be true. Surveyors customarily focus on the 2SD error (95%) as an indication of the error in most of the measurements - save a few outliers.

1) Sorta but not rigorously so for small sample size.
2) If you knew the true mean and SD of all measurements that could be made with this setup, this is strictly true. Since you only have a modest sampling of measurements, thus estimating the population mean and SD, it is only a good approximation.

3) True in the limit of large sample size.

Where's Kent when you need him? Maybe one of the other statistically enlightened posters will check my answers.

Steward Souten, post: 452146, member: 12714 wrote:

1) If I randomly pick a measurement from my data set then there is a 68.269% chance that the measurement will fall within +/- 1SD.

2) If I re-measure the distance to the target, then on the 11th time I measure it, there is a 68.269% chance that the distance measurement I
record will fall within +/- 1SD.

3) In order for the data to form a normal distribution then 68.269% of the measurements must fall within +/- 1SD.

I don't know if any of the above are true or valid but I was hoping someone in the community could help clarify.

Your thoughts?

Thanks

Hello Steward,

My understanding:

1. Roughly yes.

2. I will argue ƒ??not strictly trueƒ??. The SD you derived is only for the existing data set. Your next measurement does not have to have properties that can be forecast by the existing data set's SD; Your statistical analysis was descriptive, not prescriptive. It may sound like pedantry, but best not be making assumptions about your next measurement.

3. Sorry, not sure about this one. Intuitively it seems tautological. Kind of like saying ƒ??in order for a distribution to be normal, it must be described by one of the properties that describe a normal distributionƒ??.

I donƒ??t know if Iƒ??ll be on my own here, but I think attention to randomness in surveying measurements is overrated, and I think under most conditions randomness in measurement with modern equipment is small. Be it GNSS or TPS, noise is overcome very quickly. I think systematic biases are the larger problems that are overcome with harder work and application of reliable calibration parameters.

https://en.wikipedia.org/wiki/Standard_deviation

and confidence intervals! http://mathworld.wolfram.com/ConfidenceInterval.html

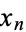
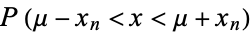0.6826895
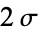0.9544997
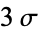0.9973002
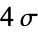0.9999366
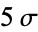0.9999994

Depends on when it was written. 1SD is bigger for a survey done with 1 chain chains than done with 100' steel tape, and so on. If you do not know what was used for the measurement the words mean nothing concrete.

Paul in PA

Note that the numbers Andy posted are for a 1-dimensional distribution. When you talk about horizontal error probabilities it's a different set of values.

I don't quite understand Paul's point. The SD will be numerically bigger if you use a sloppier measurement method, but if you have a good estimate of SD and assurance that it is gaussian normal for whatever measurement process was used, then you don't need to know anything else about the process to do statistical calculations.

Hi Conrad

Thank you for your input.

I have to be honest I am surprised that there isn't a definitive answer as to what 68.269% means in the context of my distance measurements.

To me 68.269% means in the context of my distance measurements is :-

2) If I re-measure the distance to the target, then on the 11th time I measure it, there is a 68.269% chance that the distance measurement I
record will fall within +/- 1SD - this makes a lot of sense to me because from my research the statistical analysis I performed on my distance measurements infers the probability of which SD band the next measurement will fall in.

However you stated:-

2. I will argue ƒ??not strictly trueƒ??. The SD you derived is only for the existing data set. Your next measurement does not have to have properties that can be forecast by the existing data set's SD; Your statistical analysis was descriptive, not prescriptive. It may sound like pedantry, but best not be making assumptions about your next measurement.

So for me the analysis I did was descriptive (as you pointed out) but it was also Inferential.

Even if I put distance measurements aside and said that the measurements related to one side of a table leg then even in this context what would 68.269% mean.

If I was to put the question to you Conrad how would you define 68.269% for a set of measurements?

Bill93, post: 452162, member: 87 wrote: 2) If you knew the true mean and SD of all measurements that could be made with this setup, this is strictly true. Since you only have a modest sampling of measurements, thus estimating the population mean and SD, it is only a good approximation.

Depending on your sample size, you can only say that you know the SD within some tolerance. Thus the probability of your next measurement falling in that range is 68.3% +/- something, not 68.3 precisely.

Steward Souten, post: 453169, member: 12714 wrote: Hi Conrad

Thank you for your input.

I have to be honest I am surprised that there isn't a definitive answer as to what 68.269% means in the context of my distance measurements.

Mine and Billƒ??s problem is your sample size amongst other things. Itƒ??s not exactly 68.269% probability that your next measurement will be within that range. The addition of the next measurement to your sample will also change the calculated SD again. Then with the recalculation of your new (different) SD, was your previous prediction ever really reliable?

Also a small detail is the precision with which your SD is calculated - you may have collected the data at a resolution well above the precision of the actual system generating those measurements. Your calculated SD may not be reliable. Youƒ??re also using numbers derived from a normal distribution to infer the likelihood of an upcoming event that may not belong to a normal distribution, or even belong to the same population. Have you tested for normality of your distribution?

Iƒ??m now quite sure this sounds like unnecessary pedantry to you, but I canƒ??t help it. Thereƒ??ll be some level of assumption and approximation in the advice youƒ??ll get here (RPLS) and everywhere. I donƒ??t want to add to the fuzz, if you will. Consequently some of my answers will seem to stop unsatisfyingly short of yes or no.

Anyhow, if you collect enough numbers to test your distribution is normal enough, youƒ??re satisfied all your measurements belong to the same population, and the size of your sample can overcome your sampling precision, then youƒ??ll get closer to being able to use your probability density function to make inferences about the next measurement; to being able to say thereƒ??s a 68.3% chance my next measurement will be between x and y.

I hope Iƒ??m not misunderstanding the intent of your question.

Hi Conrad

I really appreciate your insight. Your comments have certainly made me think a little deeper into this.

You have a way of picking up on things that you say are "pedantry" but they are not, your points are very logical.

I understand your point about the sample size in that if I could sample the entire population then the probability of the next measurement would be 68.269% assuming a normal distribution. So the smaller the sample size the less confidence I have in saying that the next measurement will have a 68.269% probability of falling within +/- 1SD.

(the wonderful world of surveying)

Thanks

The people that have the job to be so called professionals at quoting specifications and giving percentages of expectation to the normal people of the world are among the highest paid people out there.
Them and the psychologists that supposedly keep their minds in tune.
Of course all these numbers are to express the average expectation.
When numbers land outside what they consider the average amount, in their thinking it is you that are the problem.
I can remember when it took that certain "touch" to achieve good numbers and not the reliance upon the latest and greatest digital gizmo.