Hello Gents,
I'm a bit of a tester. I want to know for myself why a 5" total station is a 5" model. Nobody has ever explained why exactly it is a 5" model and what exactly that means. Will all angles turned be within 5", or 5" at 1 sigma? Is it 5" at random or is it systematic? how well does it point; what's the precision?
Well I decided to find out why my network adjustments often had 10" 'whoopsies' in them, even when observed under perfect conditions and repeated within seconds when reobserved. So, after establishing that my equipment and my indoor test network was stable enough to conduct angular testing I set about trying to see if there was any detectable pattern or reason why a 5" total station is always a 5" total station.
The network was groups of targets around the horizon. They were in groups of mostly 5 to determine the precision of the pointings and to keep single outliers to a minimum. If the precision was there the residuals should be the same sign and magnitude for each group. When the residuals are plotted they should appear as tightly grouped vertical lines. 700+ observations were made to try and cover as much of the circle as possible and basically just 'brute force' out any patterns or errors on the circle. To further test the hypothesis that some periodic error may be present, and seeing as how the circle was being read diametrically if all observations were reduced to a between 0-180 the pattern should still be present. The hypothesis will fail if residuals of positive and negative sign generally appear at the same section of the circle. I'll spare you the details of the least squares input stuff but here is the result:
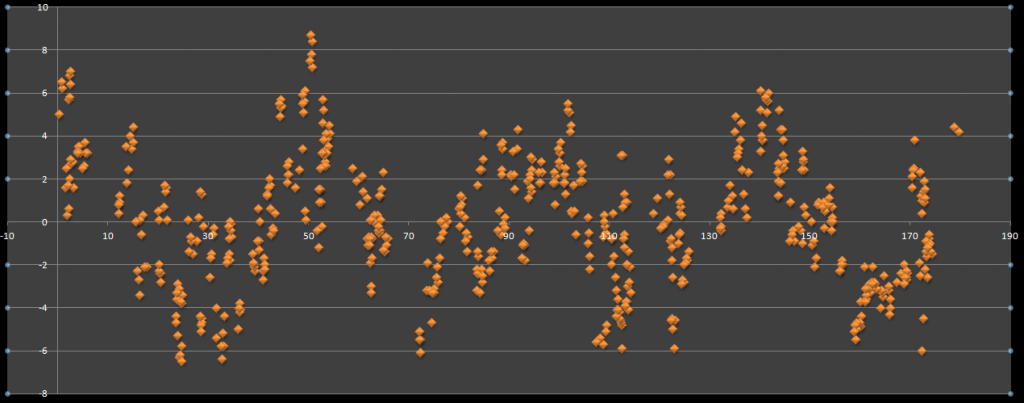
Do you agree there appears to be a pattern?
The result of the adjustment was that the group VF for directions was about 3.2" which is excellent agreement with the proposition that this is indeed a 5" total station: 3.2"*sqrt(2) = 4.5" angles. The groupings of residuals were generally very precise and around 1". So if the graph is as it seems then the error is systematic and ever-present. Some sections of the circle will ALWAYS give you a 10" error and some combinations of circle readings should give you the accuracy of an industrial total station. It looks like I could correct for angular errors by applying a function of about 5"*sin(8*C+10) which may do a good job of making this instrument perform a lot better (but I will never be bothered to!).
As always I am open to any and all criticism of my experiment, and will be more knowledgeable if someone does indeed poke holes in it. I'd much rather it be torn down than continue in ignorance.
Cheers.
2" glass 5" glass? Ambient temerature? Manual turning auto turning? You can get consistent high quality measures with a 5" gun but procedures are intensive. Great post.Hope you have time to respond.
Thanks.
Very cool
> 2" glass 5" glass? Ambient temerature? Manual turning auto turning? You can get consistent high quality measures with a 5" gun but procedures are intensive. Great post.Hope you have time to respond.
> Thanks.
Hello cutfill,
Leica 5" TCRP1205+, ambient would have been around 25*C but I didn't measure it. Manual turning. In ideal conditions the precision I can achieve with any of our 5" instruments is excellent; I can turn angles with the best of them! But if my experience and this (controlled-ish!) testing is giving true results then you pick the wrong to parts of the circle to derive your angles and you are out of luck. Sample a large enough part of the circle by rotating the instrument studs and re-observing your angles and you should improve. If your tribrach plummets are good and your station distances are far enough then you could add some extra tribrach orientations. You'd get a good sample then.
If my will is there in the future I may observe some angles and see if my correction formula can transform the instrument to a 1" instrument. I have reference marks on the instrument so I can recreate the circle orientation I used in this testing.
Cheers.
> It looks like I could correct for angular errors by applying a function of about 5"*sin(8*C+10) which may do a good job of making this instrument perform a lot better (but I will never be bothered to!).
Yes it would be interesting to derive the first order function that models the errors by Fourier analysis, remove the errors predicted by that model and see whether there are any second-order periodic errors.
The question is what the source of the errors is, i.e. whether or not it is merely a software correction in the instrument that isn't enabled (seem quite possible) or that actively dithers output. Without knowing the details of how the circles are etched, I have say that it seems unlikely that the same master isn't used in etching all of the circles in the line, regardless of final accuracy claimed. So, given the periodic nature of the error, some software correction strikes me as more likely.
Hello Kent,
And that is why I went looking through our service reports the other day when I was sure the up to 10" error was real and present. There are values in the report for:
H1 eccen. phase
H1 eccen. ampl.
H2 eccen. phase
H2 eccen. ampl.
H1 circle table corr.
H2 circle table corr.
and in our 5" instrument these values happen to be respectively:
000.0
0.0
000.0
0.0
No
No
I suspect Leica know EXACTLY what errors affect the circles, and if it is a regular function(s) then deriving the corrections at the factory would be child's play after sampling a circle at a few selected points.
From Leica's own literature I know the high accuracy industrial total stations are bigger circles and are sampled at 4 points for a reading. They are made as good as can be, it seems.
Cheers.
> I suspect Leica know EXACTLY what errors affect the circles, and if it is a regular function(s) then deriving the corrections at the factory would be child's play after sampling a circle at a few selected points.
>
> From Leica's own literature I know the high accuracy industrial total stations are bigger circles and are sampled at 4 points for a reading. They are made as good as can be, it seems.
Am I mistaken in thinking, though, that the other higher precision instruments in the same series as yours all have the same diameter circle? That's what makes me think the same circle is probably used all across the series.
Your instrument is claimed to have an absolute circle, I believe. Is that what you understand?
> Am I mistaken in thinking, though, that the other higher precision instruments in the same series as yours all have the same diameter circle? That's what makes me think the same circle is probably used all across the series.
>
> Your instrument is claimed to have an absolute circle, I believe. Is that what you understand?
Sorry for the misunderstanding Kent - yes the 1200+ series comes in 1", 2" 3" and 5" flavors, all outwardly look the same and should use the same size encoder circle.
I was referring to a different family of instruments which are offered as 0.5" instruments: TDRA6000, TS30 etc. These are made with a new, bigger standard to house the bigger circle (~15%).
Thanks Shawn,
Part of it was to fight my own ignorance about errors (or not) in modern total stations and to determine if the 'errors' i was seeing in my adjustments were really actually errors.
> Sorry for the misunderstanding Kent - yes the 1200+ series comes in 1", 2" 3" and 5" flavors, all outwardly look the same and should use the same size encoder circle.
>
Yes, so the question is what really the differences between the four different models in the 1200+ line are, whether they are entirely the product of software corrections or otherwise. What you've posted suggests to me that the instruments are mechanically similar, that the differences are in how the software makes corrections.
One interesting question that arises is whether after modeling the cyclic error in the angles one could actually improve results by applying corrections in *post-processing*. I'm thinking "yes".
I can also add some extra information gleaned from the experiment.
tribrach re-clamping in each stud position consistently produced values around the 0.04 to 0.05 mm mark from one point to the next regardless of where the instrument was in the network meaning the centre of the telescope was going around the centre of the tribrach at a radius of 0.025 mm or so. Very small difference.
The reflectorless EDM in this 1200+ instrument produced a group VF of around 0.7mm in this test network to white paper at many varying angles. This precision is excellent and confirms the field results I've been seeing for years. The ageing (died today actually) TCA1105 I also tested returned below 1 mm precision for small reflective tape squares in the (mostly) same network. This instrument is specced to somewhere worse than 2 mm accuracy for reflective tape if I remember correctly.
The calculated distance between my laser printed target groups came in at an average of 9.97 mm (10 mm design) at a stdev of 0.06 mm. This is either a good result for the printer, or the ability of the total station to establish a good scale for the network vide the EDM.
Explain A 10" Whoopsie
Whoopsie, you think you have a problem, but are not explaining it well.
You think you have a scientific observation process, but have not explained it at all.
I regularly use a 5" gun, using D&R and 2D&2R observations. It does not phase me that a spread may even be 20" apart, at the end of the day, I find very acceptable traverse closures prior to any adjustment. Some setups just fall into perfect order and some do not. Target orientation, sun, shadows, background, quite a few things can affect any field observation.
You have pretty much proven you have an acceptable 5" gun. That there is a 45° pattern could lead to various compounded circle errors, but I surmise that the circle making machine has tolerance limits and readjusts itself during the process. It probably has good days and bad days.
I rented a 5" total station once while mine was in for repair. I could not explain a few wild spreads until I carefully watched my readings as I turned the adjustment knob. I would see something like 11", 12", 13", 33", 34" 35". A 20" jump in the circle reading and it repeated every minute. No one could explain it at the shop, but I would say electronics not mechanical. I returned it, did not pay for the rental, and borrowed a 5" reading instrument and got better results.
If we are to truly learn something from your endeavor a more thorough explanation is required.
Paul in PA
Explain A 10" Whoopsie
Hello Paul,
My own definition of a "10" whoopsie" was when in a network adjustment I would see directions in the same set cop residuals of of 4"-9" but opposite in sign when everything else hovered around a few seconds. So the adjustment had changed my derived angle by about 10". These were larger networks where the shape is very tightly controlled by the excellent specs of the EDM.
I had a 10" moment just recently when turning sets. In good conditions I had the robot turn 2 sets. reduced angle was about 120*00'00". Just for kicks I turned the instrument studs around and did the sets again. 120*00'10". Turned the studs. 120*00'00". Turned them back to the 'bad' postion: 120*00'10", again. Turned to a 'good' position: 120*00'00", again. Turned the tribrach to 10* off 'bad' orientation: 120*00'06". Back to 'bad' orientation: 120*00'10". Turned it by eye just to check.
I was seemingly getting a systematic error from the circle, and it was perfectly repeatable. So I set about to see if I could quantify the useful, real-world accuracy of the total station, and to see if it was really within spec, and possibly what determines the spec. Turns out, as disappointed as I am, that the instrument is performing to spec, and it's possibly a spec that can't be meaningfully improved upon by more sets or more pointings.
Most people I talk with are not aware, or give any indication of being aware, of what 5" means in terms of real world angles. And the title was expressing, in a silly way, my disappointment (and I reckon others disappointment if only they knew) that a 5" second instrument really only guarantees you of about 15".
I definitely didn't fully explain all the details of the methodology as I didn't have the time, didn't want to exceed the word limit and hoped the target audience trusted the methodologies and precision I determined in earlier experiments. I have thought of another couple of procedures to verify my interpretation of an error with amplitude and phase components, but this time I'm not sure I can achieve or control for the positional accuracy required.
As I've already stated, I'm in it to fight my ignorance as much as anything. If a guru were to post that residuals like that are a normal artefact of a least squares adjustment, and explain why I've found nothing, then I'd be perfectly happy, or even happier as I've gained some more knowledge. But it would also leave unexplained exactly what makes a 5" total station such. That's why I'm thinking of another way to verify the results at a different scale; to try and 'ride the wave' of any cyclic error.
Cheers.
What you've done iswhat I've understood goes into higher order instruments with identical construction. Or at least similar to it. Beautiful work.
Why do you suppose there are four periods in th graph?
"The network was groups of targets around the horizon."
First off, I'll say I admire your stamina in taking that much data. I once considered doing such an experiment and didn't carry through.
But I'd like a little more information about your setup. Without knowing more about that, one can't think about possible reasons the setup could contribute to the pattern.
Although you talk about turning the instrument in the tribrach, I think you probably didn't do that during the 700 measurements. I think you measured angles with the instrument in one setup, all on one face of the instrument, with many combinations of targets as backsight and foresight. Right?
How many targets and groups? What approximate angles between groups?
Did you take one angle measurement for each of the 700+ pairs of 37 or so targets, multiple measurements of fewer targets, or what?
What was the advantage of groups over randomly placed targets?
-----
Prior threads on this forum have discussed what a spec of X degrees means for an instrument. Unfortunately, I don't have time this morning to link those threads.
Basically, the spec is the tolerance for pointing at one target, averaged direct and reverse to take out systematic errors. Two pointings D&R make an angle with 1.4 X tolerance. 2D2R gets you an angle with tolerance X.
> The network was groups of targets around the horizon. They were in groups of mostly 5 to determine the precision of the pointings and to keep single outliers to a minimum.
Confused. "groups of targets"?
What were the groups? Every 1 degree around the horizon? 5 degrees? Can you share a photo of the target groups? I'd like to try this myself.
Would have been interesting to see the results when completed manual testing to redo in robotic mode.
> And that is why I went looking through our service reports the other day when I was sure the up to 10" error was real and present. There are values in the report for:
>
> H1 eccen. phase
> H1 eccen. ampl.
> H2 eccen. phase
> H2 eccen. ampl.
> H1 circle table corr.
> H2 circle table corr.
>
> and in our 5" instrument these values happen to be respectively:
>
> 000.0
> 0.0
> 000.0
> 0.0
> No
> No
>
> I suspect Leica know EXACTLY what errors affect the circles, and if it is a regular function(s) then deriving the corrections at the factory would be child's play after sampling a circle at a few selected points.
After thinking about that a bit, it looks to me as if your instrument is designed to model the effect of the eccentricities of the pairs of circle reading points as a first order harmonic by specifying the phase (angle) at which the effect of the eccentricity is zero and the amplitude of the error. Those would be the H1 values.
The H2 values probably correspond with the other pair of circle reading points.
The H1 and H2 circle table corr. values are, I assume, a lookup table that makes some additional corrections beyond those output by the harmonic model. I'd guess that those capture both circle graduation errors and variations in eccentricity from the machining of the center.
It may well be that the difference between the various instruments in the Leica TCRP 1200 family is just in the software corrections, the cost of calibration needed to derive the values used in the software corrections being what accounts for the differences in price. For example, the next step up from the 1205+ could enable just the first-order harmonic corrections and the top of the line has both harmonic corrections and a very good lookup table in memory.
I Would Say, Plotted Target Points On A Target
Plot a target with 5 exactly equal distances apart targets that can be readily viewed simultaneously within the scope. Backsight the first target, record 4 more by fine tuning the knob, turn to next target group, record 5 and so on.
Placing these target on 4 interior walls it is easy geometry to get the angular separation between points on a target with a spread sheet. In fact one may prefer to adjust all 5 target observations to the first point's angle using simple geometry, then look at the big picture.
Paul in PA



