There are 4 points, (14, 13, 321 and 322):
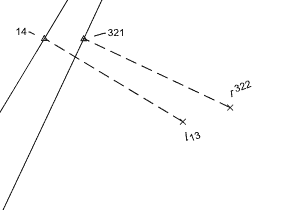
321 wants to be where 14 is and 322 wants to be where 13 is.
Coordinates are known for all four points, and 321..322 is N73-17-19E, and 14..13 is N76-38-08E.
Of course, one could, using COGO, translate and rotate, to align. But, if one wanted to estimate (or calculate as closely as possible), where the center of the circle would be, such that if one of the lines was rotated on an arc of that center point, the two would align very closely?
My first thought was to extend each line until they intersect; measure that length; then draw a circle with it's center at the mid-point of a line drawn between the midpoints of the two lines, and find a point along that arc that is perpendicular to that drawn line. (Does that make sense?).
But if there's a geometric solution, there must be a mathematical solution too.
Or, is the solution indeterminate?
I've solved similar problems before in mechanical assemblies (think "two-bar" mechanisms, such as a trunk hinge), but can't quite get my head around this one.
I don't think you are going to find an exact solution unless the lengths of the lines are some magic relative values that work with the difference in angle. You are giving us 3 variables (radius point x,y and rotation angle) to fit 4 values (x,y difference for each of two point sets).
Nor have I heard of a "standard" method of approximation. Give us coordinates for the points so we can play with approximations using least squares.
Okay....14 to 321 is the "Chord". Delta is the difference in bearings ie azi(14 to 13) minus azi(321 to 322). solve for the Radius
Long chord = 2R(sin(delta/2))
2R=LC/SIN(d/2) solve for "R"
Calculate the center of the circle. You might go halfway from 14 to 13 then go perpendicular the distance of R(cos(d/2)) to get your centerpoint.
Give me some numbers, and I'll solve.
I believe the intersection of the perpendicular bisectors of the two error vectors will give you the point to rotate about (spent too much time in my early days looking for busted traverse turns)
A mathematical general least squares solution:
.. assuming that the precision of coordinates 13 and 14 are the same
and that 321 and 322 are the same
1. determine directional difference between lines 321-322 and 14-13
theta = dir(321-322) - dir(14-13)
2. rotate points 321 and 322 so that they align with line 14-13
a. Xr(321) = X(321)cos(theta) - Y(321)sin(theta)
Yr(321) - X(321)sin(theta) + Y(321)cos(theta)
b. Xr(322) = X(322)cos(theta) - Y(322)sin(theta)
Yr(322) - X(322)sin(theta) + Y(322)cos(theta)
3. determine mid points between
a. 14 and 13 => 15
b. r(321) and r(322) => r(333)
4. determine mid point coordinate differences
a. dX = Xr(333) - X(15)
b. dY = Yr(333) - Y(15)
5. translate 321 and 322
a. Xt(321) = Xr(321) - dX
Yt(321) = Yr(321) - dY
b. Xt(322) = Xr(322) - dX
Yt(322) = Yr(322) - dY
Tom Adams, post: 328754, member: 7285 wrote: Okay....14 to 321 is the "Chord". Delta is the difference in bearings ie azi(14 to 13) minus azi(321 to 322). solve for the Radius
Long chord = 2R(sin(delta/2))
2R=LC/SIN(d/2) solve for "R"Calculate the center of the circle. You might go halfway from 14 to 13 then go perpendicular the distance of R(cos(d/2)) to get your centerpoint.
Give me some numbers, and I'll solve.
Gotta go get some Ibuprofen, but in the meantime....:
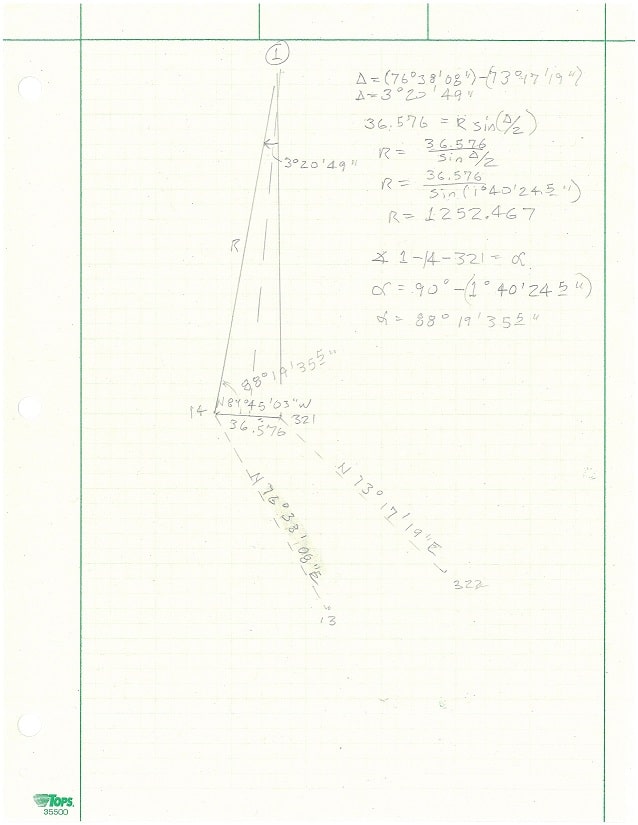
I inversed (with a calculator) from 321 to 14 and got N 89å¡45'03"W a distance of 36.576. Assuming I inversed correctly, I solved it accordingly. I did no checks and no other inverses, but following is what I came up with.
Call 14 to 321 the long-chord. Delta is the difference in bearings of the two lines. I solved for "R" and the angle @ 14. Turn the angle @ 14 and go distance R. Turn the opposite angle @ 321 and go distance "R" and you should get the same point. Also you could do a similar check from 13 to 322 and I think you should get the same point 1. I didn't use a software, so I didn't go through all my inverses and checks. If I made a mistake, the principle is the same.
Tom Adams, post: 328767, member: 7285 wrote: I thought 321 needed to be 14?
Will ya look at that! It's a typo. Thanks for noting that.
MLSchumann, post: 328758, member: 471 wrote: A mathematical general least squares solution:
.. assuming that the precision of coordinates 13 and 14 are the same
and that 321 and 322 are the same
I didn't realize least squares could be used to find blunders (which, i thought it was obvious this is).
I thought least squares was meant to find the "most probable" location of two points (or the several observations of the same point), that are (presumably) very close together.
If your calculation is meaning the locations of each of the pairs, then I'm not sure this would be an appropriate solution. If I'm mis reading the calc, please advise.
rfc, post: 328748, member: 8882 wrote: There are 4 points, (14, 13, 321 and 322):

321 wants to be where 14 is and 322 wants to be where 13 is.
Coordinates are known for all four points, and 321..322 is N73-17-19E, and 14..13 is N76-38-08E.
Of course, one could, using COGO, translate and rotate, to align. But, if one wanted to estimate (or calculate as closely as possible), where the center of the circle would be, such that if one of the lines was rotated on an arc of that center point, the two would align very closely?My first thought was to extend each line until they intersect; measure that length; then draw a circle with it's center at the mid-point of a line drawn between the midpoints of the two lines, and find a point along that arc that is perpendicular to that drawn line. (Does that make sense?).
But if there's a geometric solution, there must be a mathematical solution too.
Or, is the solution indeterminate?
I've solved similar problems before in mechanical assemblies (think "two-bar" mechanisms, such as a trunk hinge), but can't quite get my head around this one.
hello rfc,
tom has the answer i was going to give. the only difference being that the least squares solution (the one that gives the minimum sum of the squared residuals after the transformation) would be the calculation of the center of the circle using the chord joining the midpoints of the lines.
Tom Adams, post: 328786, member: 7285 wrote: I inversed (with a calculator) from 321 to 14 and got N 89å¡45'03"W a distance of 36.576. Assuming I inversed correctly, I solved it accordingly. I did no checks and no other inverses, but following is what I came up with.
Call 14 to 321 the long-chord. Delta is the difference in bearings of the two lines. I solved for "R" and the angle @ 14. Turn the angle @ 14 and go distance R. Turn the opposite angle @ 321 and go distance "R" and you should get the same point. Also you could do a similar check from 13 to 322 and I think you should get the same point 1. I didn't use a software, so I didn't go through all my inverses and checks. If I made a mistake, the principle is the same.
Thanks, guys. That's cool. I'm looking at a couple of points that are near that distance away from the subject points (around 1100 feet) and at about the correct azimuth relative to them.
If I can't find some busts in the angles turned there, I'll head back and do them again, or possibly look at running some cross ties.
Appreciate the help.
rfc, post: 328800, member: 8882 wrote: I didn't realize least squares could be used to find blunders (which, i thought it was obvious this is).
I thought least squares was meant to find the "most probable" location of two points (or the several observations of the same point), that are (presumably) very close together.If your calculation is meaning the locations of each of the pairs, then I'm not sure this would be an appropriate solution. If I'm mis reading the calc, please advise.
For rfc
I'm confused!
First, it is not in any way obvious that this is a "blunder" detection exercise. More information about the situation is needed in order to be able to ascertain the objectives. How did 13 and 14 come about and how did 321 and 322 come about and what is the relationship?
The implication from the statement "321 wants to be where 14 is and 322 wants to be where 13 is" is that a transformation is desired.
Confusion is introduced by the call for a circle. Why a circle and what purpose does it serve in attaining the objectives? What are the objectives?
More confusion arises with the paragraph:
"My first thought was to extend each line until they intersect; measure that length; then draw a circle with it's center at the mid-point of a line drawn between the midpoints of the two lines, and find a point along that arc that is perpendicular to that drawn line. (Does that make sense?)."
- - Does that make sense = NO!
Did geometry and mathematics take on new definitions?
"But if there's a geometric solution, there must be a mathematical solution too."
- - Geometry is a branch of mathematics. As a consequence, a geometric solution is a mathematical solution!
My confusion increases as I re-read the original post and read each posted reply. Perhaps someone will draw a complete picture that presents the problems using black and the solutions using red? Annotations explaining relevant related issues would be helpful. Since it is implied a transformation was not desired, then, what was desired? Why?
MLSchumann, post: 328856, member: 471 wrote: For rfc
I'm confused!
First, it is not in any way obvious that this is a "blunder" detection exercise. More information about the situation is needed in order to be able to ascertain the objectives. How did 13 and 14 come about and how did 321 and 322 come about and what is the relationship?
All good questions. As a student of surveying, I know there are many here more competent to answer some of them, but I'll try.
MLSchumann, post: 328856, member: 471 wrote: The implication from the statement "321 wants to be where 14 is and 322 wants to be where 13 is" is that a transformation is desired.Confusion is introduced by the call for a circle. Why a circle and what purpose does it serve in attaining the objectives? What are the objectives?
By way of general explanation:
Let's say you have a traverse that's gone bust, like this example. Point 18 "should be" where point 10 is. A year ago, before I even knew what least squares was, upon completing a traverse with blunders, several here pointed out a couple of techniques to troubleshoot traverses gone bust.
The first was to determine whether one might have blown a distance measurement, or an angle measurement. The advice was to look for two points approximately (or exactly) parallel to the non-closing points. In this example, it'd be 14 and 15. If a distance measurement error existed there, it could be the reason 10 and 18 don't close.
Or, let's say angle 13-14-15 was blown. An arc with 14 at it's center, and the measurement of the subtended angle between 14 and 10 and 14 and 18, might point to an angular bust there.
But in the current case, I happened to have a large portion of a traverse that wasn't closing (by a large amount), but what made it unique is that I had side shots to other points that I knew were good. In effect, I had two lines that, in order to "align" them, meant both translation and rotation.
That just got me thinking that a surveyor might use this information on it's own to predict a point about which a portion of the traverse might be rotated, that would satisfy both the angular and linear requirements for close alignment. As Tom pointed out, once that's done (or during the process), least squares could be applied to predict the uncertainty of the solution.
My interest in seeing if this was so, was initially purely academic, nothing more. I'm always fascinated (and impressed) by the depth and breadth of knowledge here. As it turns out, there may in fact be some practical application for the solutions presented.
MLSchumann, post: 328856, member: 471 wrote:
More confusion arises with the paragraph:
"My first thought was to extend each line until they intersect; measure that length; then draw a circle with it's center at the mid-point of a line drawn between the midpoints of the two lines, and find a point along that arc that is perpendicular to that drawn line. (Does that make sense?)."
- - Does that make sense = NO!
As I said, this grasshopper's ability to describe things using the proper terms is way less than others' here. Sorry for the inadequacy. In my own defense though, I'd say I've gotten a heck of a lot better than I was a year ago, when I began my studies.
MLSchumann, post: 328856, member: 471 wrote:
Did geometry and mathematics take on new definitions?
"But if there's a geometric solution, there must be a mathematical solution too."
- - Geometry is a branch of mathematics. As a consequence, a geometric solution is a mathematical solution!
Understood. I see the point.
MLSchumann, post: 328856, member: 471 wrote: My confusion increases as I re-read the original post and read each posted reply. Perhaps someone will draw a complete picture that presents the problems using black and the solutions using red? Annotations explaining relevant related issues would be helpful. Since it is implied a transformation was not desired, then, what was desired? Why?
A transformation alone would not have solved the problem, because there was clearly angular mis-alignment apparent as well.
I assumed you were trying to figure out how to rotate a closed figure into a common bearing base. But the principle is the same. In the example above, with the broken traverse, I would inverse from 10 to 18 and 10 to 14 and I would look @ the difference in bearings (ie the angle 10-14-18. If the two distances are equal to each other and the angle @ 10 is close to an even angle, I would zero in on that being the "busted" angle. I would also inverse from 10 to 18 and see if it is parallel to the 14-15 bearing and if it's close to an even distance (say 10') I would look to see if I have a busted distance on that line. (Oh and I meant to add that if you turned the closing angle and added them all up and subtracted what that angle should be, you should get the same angle that matches the angle 10-14-18. That would be the first step adding all the interior angles, and seeing if they total (n-2)*180, where "n" is the number of angles.)
As to least squares being used to find blunders, it can absolutely be used to do that. I always liked looking for blunders the old-fashioned way. At least doing that for a while develops an understanding that helps you see what the least squares is doing.