> Please note the 2 lb. hammer in the first photo, used to make small adjustments.:-)
I believe it's often affectionately referred to as the "least squares adjustment tool". 😀
World's Smallest Traverse? Plotted Error Ellipses
And adjusting it with:
Pt. 67 = 63
Pt. 66 = 62
Pt. 65 = 61
Pt. 68 = 64
Gave this fairly stunning confirmation of the precision of the shifts of the instrument center by tilting the tribrach footscrews:
[pre]
From-To Bearing mmx10^-2
61-64 N88-04W 16.82
62-64 N25-02E 16.83
63-64 S25-41E 16.82
[/pre]
Azimuth was probably about right for eyeballing.

World's Smallest Traverse? Plotted Error Ellipses
Thanks Kent, it looks like a good result.
I will try and get some results with the compensator on. I turned it off because I was unsure what effect it would have on the angle readings, and whether they were wanted. It shouldn't make much difference but I didn't note how far off the horizon the targets were for this particular setup so I can't attempt to quantify how much of a difference it would have made. The targets were on the horizon when I set them but I moved slightly for this setup. As a good scientist I will report any significant differences, otherwise I'll probably just report 'no detectable change'.
World's Smallest Traverse? Plotted Error Ellipses
>It shouldn't make much difference but I didn't note how far off the horizon the targets were for this particular setup so I can't attempt to quantify how much of a difference it would have made.
Yeah, I wouldn't expect a significant change at all since all one care's about here are coordinates relative to 99. That is a much less geometrically demanding situation than trying to calculate absolute coordinates in relation to the targets.
One thing I've been meaning to test in Star*Net is whether adding one more target at nominally 90 would make a significant reduction in the size of the semi-major axis of the error ellipses.
World's Smallest Traverse? Plotted Error Ellipses
>
> One thing I've been meaning to test in Star*Net is whether adding one more target at nominally 90 would make a significant reduction in the size of the semi-major axis of the error ellipses.
A network simulation revealed adding a double target at 90 degrees did reduce the northing component of uncertainty by about 23% but did not make the error ellipse circular like adding a target at 270 degrees would have. My 270 degrees wall is about 5-6m away so it may not actually increase the precision of the results.
> Way cool Conrad, you have stepped into the world of metrology 🙂
>
Thanks gschrock, I'm a practicing licensed/registered cadastral surveyor, but I'm a measurement geek also. We had a good training in least squares, networks, precision surveying, etc. at uni and I've always had an interest in it since. Least squares, close range photogrammetry, combining GPS and TPS in survey, monitoring, machine alignment etc. all interests me, with the only problem being that there is hardly ever any call for it.
World's Smallest Traverse? Plotted Error Ellipses
> A network simulation revealed adding a double target at 90 degrees did reduce the northing component of uncertainty by about 23% but did not make the error ellipse circular like adding a target at 270 degrees would have. My 270 degrees wall is about 5-6m away so it may not actually increase the precision of the results.
2 targets at nominally 90 degrees + 1 at 270 degrees nominally 5m distant would do the trick, though.
World's Smallest Traverse? Plotted Error Ellipses
>
> Yeah, I wouldn't expect a significant change at all since all one care's about here are coordinates relative to 99. That is a much less geometrically demanding situation than trying to calculate absolute coordinates in relation to the targets.
>
As expected, not much change. Actually it made the sides of the triangle agree with the calculated theoretical distance more or less exactly. The setup was a bit below the targets so the compensator made a slight difference, which in this solution looks like a scale, which would depend upon how far above or below the horizon the targets were. Less care was taken this time to see just how sensitive the solution was.
I also tried 'traversing' back in at 40" increments just to see. The relative angles only need to be out by a few seconds to cause the variation from the exact geometrical shapes.

OK, I think I'll just stop now.
This will do me for this experiment. Just downsized to a 60" triangle which is roughly 0.065 mm from centre. Still looks like a triangle.
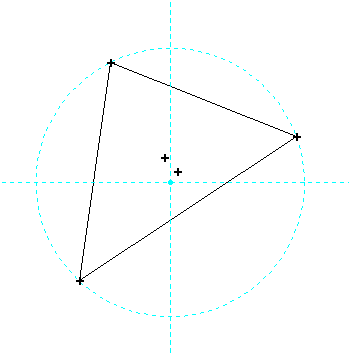
Thank you Conrad and Kent.
You have both increased my wisdom.:beer:
> Thank you Conrad and Kent.
> You have both increased my wisdom.:beer:
Your heart (and gratitude) is in the right place, but make no mistake, what you may have learned from this thread was knowledge, not wisdom.
Don



