Hello Gents,
Out of my recent "why your 5" total station sucks" thread came a result which looked like a circle graduation periodic error which looked like it fit neatly, several times, into exactly 180* or 360*. It looked like you may be able to fit a sine function which would remove a fair portion of what is probably the major harmonic, or the first, dominant term of a fourier series.
I thought about how to overcome this 'error', and applying the function to individual directions. That would probably work. I also wondered if the position of the 3 studs of the instrument had a relationship with a sine function. Well, turns out it does, as (i think) any other even division of 360. So if you plot any 3 points on a sine curve 120* apart the distance from the X-axis sum to zero. Like this: sin(0)+sin(120)+sin(240)=0+0.866-0.866=0. Likewise sin(23)+sin(23+120)+sin(23+240)=0.39+0.60-0.99=0. And so do the other numbers I tested.
So if you read an angle in the 3 stud positions, any periodic error which repeats an exact multiple of 2 in 360* then you should eliminate that error. The error I measured seemed to be 8 times in 360, and it works out that sin(8*A)+sin(8*(a+120))+sin(8*(A+240))=0 also.
I looked for literature on long period graduation errors and the one I found seemed to suggest a wavelength of 360* was normal. So I started thinking of why the 'error' in my Leica was 8 times and not just an easy 1 x 360*. Well if you have a wavelength of 360* then turning the telescope 180* will mean you are always riding the sine wave on the equal and opposite side, meaning your errors will cancel perfectly. So if you intentionally introduce a periodic error of 360* to create a spec then turning the telescope will eliminate it perfectly. But, if it is a multiple of 2 then the second face will be riding the sine wave exactly in phase with the first face and you can't eliminate it.
So introducing a period error of 360/2 or 4 or 8 etc. will ensure a spec which cannot be overcome by two face readings. Make it a decent number like 4 or 8 and you'll get pretty good seemingly random errors everywhere on the circle. But ride this function at 3 points exactly 120 apart and you should eliminate it. surveythemark seemed to confirm in my last thread that all of the recent Leica instruments could be 1", but software decided if it was a 1", 2", 3" or 5". So I imagined that they print the circles knowing they'll come out with a (regular??) pattern 'error' which is corrected for if you pay for the top models. Even if this is not intended, my experimentation seemed to show a regular wave anyway. The reverse could also be true: if the circle is perfect and the instrument applies a regular function error then the effect is the same.
I posit, without proof, on nothing else but my experimentation and about 2 hours worth of thought, that if you own a total station with a periodic graduation error on the circle which resembles our Leica, that if you observe an angle in each of the three stud positions, you can eliminate a worthwhile portion of the periodic error.
I banged this all together pretty quickly to throw it out there to you guys. I may have overlooked something big so I'm preparing to be embarrassed.
Cheers.
> I posit, without proof, on nothing else but my experimentation and about 2 hours worth of thought, that if you own a total station with a periodic graduation error on the circle which resembles our Leica, that if you observe an angle in each of the three stud positions, you can eliminate a worthwhile portion of the periodic error.
>
Could this be confirmed by performing the following simple test?:
1. Set up the instrument and a single target group consisting of two fairly close targets (say one of your strips).
2. Take multiple pairs of measurements, (D&R), mean them and reduce them using least squares.
3. Do the same thing as in 1. above, but this time, use only one face, but rotate the instrument in the tribrach. Mean and reduce.
4. compare results.
> Could this be confirmed by performing the following simple test?:
> 1. Set up the instrument and a single target group consisting of two fairly close targets (say one of your strips).
> 2. Take multiple pairs of measurements, (D&R), mean them and reduce them using least squares.
> 3. Do the same thing as in 1. above, but this time, use only one face, but rotate the instrument in the tribrach. Mean and reduce.
> 4. compare results.
Hello rfc,
The second test I devised for mapping a long periodic error was an outside test requiring a perfect, still observing day.
Lay out an angle of about 22* from station A by placing station B and C about 22* apart and about 200 m away. Make the distance to B and C result in B and C being exactly the unit wavelength of your EDM apart. Set up on a point D which is in-line with B and C and measure the distance between B and C with the one carrier and prism. this will eliminate EDM constant error and cyclic error. You should have a distance between B and C which will, by simple trig, give you an angle B-A-C which could be sub-second accuracy. This is your standard.
Set up on A and measure B-A-C . Record in face left and separately in face right so you've now covered 2 parts of the circle. Unscrew tribrach and rotate about 11*. Re-clamp, re-center, re-level and observe again. If a large (measurable) cyclic error is present in the graduations you should see the angle B-A-C grow, stabilise, shrink, stabilise, grow and so-on-and-so-forth. You could figure out an approximate amplitude for the error by adding up all the differences you get during one growing run and dividing by two. You could also check to see if the pairs of FL/FR readings when averaged gave the true angle.
I hope this makes sense.
edit: 22* may not be the best angle depending on the period of the error. A bigger or smaller angle might be better, but just not too small.
> I looked for literature on long period graduation errors and the one I found seemed to suggest a wavelength of 360* was normal. So I started thinking of why the 'error' in my Leica was 8 times and not just an easy 1 x 360*.
Did you by any chance find a better description of the circle design and reading method than the one given in the following paper by some Croatian geodesists? The paper discusses a Leica circle encoding and reading system used in the TPS1100 series, which I gather has a circle reading system design that is similar to that of the 1200 series.
file:///C:/Documents%20and%20Settings/User1/My%20Documents/Downloads/KiG7a_Solaric_N.pdf
Note that the actual circle graduations read by the instrument are the gaps of transparent circle between opaque mask and vary in width, with every 8th gap (or "crack" as the authors call it) being significantly wider.
The other feature is that the widths of the gaps vary to form all 128 binary numbers from 0 to 128, i.e. 000000 to 1111111, so the circle itself has some significant variations.
>
> file:///C:/Documents%20and%20Settings/User1/My%20Documents/Downloads/KiG7a_Solaric_N.pdf
Hello Kent,
That link looks like it's to your own hard drive, which I can't see.
> That link looks like it's to your own hard drive, which I can't see.
Yes, sorry about that, and while we're at it, let's make that:
>"The other feature is that the widths of the gaps vary to form all 128 binary numbers from 0 to 127, i.e. 0000000 to 1111111, so the circle itself has some significant variations."
http://hrcak.srce.hr/index.php?show=clanak&id_clanak_jezik=20127
>
> Did you by any chance find a better description of the circle design and reading method than the one given in the following paper by some Croatian geodesists? The paper discusses a Leica circle encoding and reading system used in the TPS1100 series, which I gather has a circle reading system design that is similar to that of the 1200 series.
I digested as much as I could find on the 1100 series some years ago now, so if I had seen/browsed that document I have forgotten now. That's as detailed a description as I recall seeing. Usually I just remember documents going no further than circle... coded track... light... CCD... absolute angle!
Nice find.
If, as would appear, the Leica circle varies in its net masking properties as the sectors with binary numbers that have more zeros than ones coded into them (i.e. significantly less transmissive circle for the light source to pass through since the gaps representing 0 are narrower than those for 1), then I'd think that the net light level at the CCD pixels would show periodic variation around the circle. That may produce a non-linear output from the CCD that shows up as a periodic error.
It may also explain why particular parts of the circle seem to give more consistent results (smaller relative RMS error in the neighborhood of some angle value).
> If, as would appear, the Leica circle varies in its net masking properties as the sectors with binary numbers that have more zeros than ones coded into them (i.e. significantly less transmissive circle for the light source to pass through since the gaps representing 0 are narrower than those for 1), then I'd think that the net light level at the CCD pixels would show periodic variation around the circle. That may produce a non-linear output from the CCD that shows up as a periodic error.
The paper doesn't mention using the net light level for measurement. The linear CCD array is only determining the centre of each of 10 gaps, including 0 and 1 gaps on both sides of the rough division start gap (the big one). It doesn't matter that they vary in width as they are printed with consistently spaced centres all around the circle. The values for the gap centres is what is calculated, reduced to a centre number, and averaged for the further enhancement of precision over the determination of angle from just the centre of the rough division start gap.
The system is designed to be able to detect the position of the circle to 0.3 mgon (0.09"). The precision involved is immense. I can't imagine that the 'errors' in the circle are anything but known and controlled. There is nothing about the angle detection system, as described, that lends itself to systematic and periodic errors.
You may be onto something, but I can't see the specific mechanism of such an error.
I don't know if this will help, but here's a graph of the number of 1's in the binary number to represent each of 128 segments of a circle.
Hello Bill,
If you read the description of the angle reading mechanism, you'll find it doesn't use the net value of light on the whole of the CCD array for anything. After determining whether each slit is a 1 or a 0 or an interval divider, the system then only cares about the position of the centre of the individual slits.
True, but I was hoping the picture would inspire some other ideas. (And I needed something to occupy me until I felt like going back to sleep.)
I'd be interested to see a graph of your data that was posted on the [msg=293780]other thread[/msg], with the sine function subtracted.
It would seem to me that it would be easier to calculate this than to rotate the instrument in the tribrach, which poses some risk of disturbing the centering.
> The paper doesn't mention using the net light level for measurement.
How do you interpret this bit?
"Light falling through a certain crack falls on several pixels. Voltages on the pixels of the linear CCD are read with the use of a multiplexer and A/D^3 converters, and based on these volages the amount of light which fell on them can be calculated. This enables to determine how big part of the pixels light falls, and exact determination the centre of crack through which light falls."
> You may be onto something, but I can't see the specific mechanism of such an error.
>
> I don't know if this will help, but here's a graph of the number of 1's in the binary number to represent each of 128 segments of a circle.
> 
That's very interesting. I'd particularly like to see what that graph looks like with the interval from 180 to 360 superimposed on 0 to 180 as Conrad did.
The widths of the transparent gaps in the circle vary from 60µm to 180µm
Wide = 180µm
1 = 120µm
0 = 60µm
What would be interesting would be to graph the ratio of transparent gap widths to opaque mask for the 128 components around the full circle, in effect the "opacity" of the circle through which the light source passes first.
> I'd be interested to see a graph of your data that was posted on the [msg=293780]other thread[/msg], with the sine function subtracted.
>
One feature that Conrad's graph had is that the rising limbs of the graph appear to be steeper than the falling limbs, a sort of mirror image pattern of what your graph of the frequency of ones has.
> > The paper doesn't mention using the net light level for measurement.
>
> How do you interpret this bit?
>
> "Light falling through a certain crack falls on several pixels. Voltages on the pixels of the linear CCD are read with the use of a multiplexer and A/D^3 converters, and based on these volages the amount of light which fell on them can be calculated. This enables to determine how big part of the pixels light falls, and exact determination the centre of crack through which light falls."
Good morning Kent,
Not that it would affect the discussion much, but wide gaps are zeroes and thin are ones which means more light the more zeroes.
That paragraph you posted mentions the array being read with a multiplexer. A multiplexer allows for fetching and single line (pixel) to send as output. From Wikipedia:
>An electronic multiplexer makes it possible for several signals to share one device or resource, for example one A/D converter or one communication line, instead of having one device per input signal.
It's job seems to be fetch from each individual pixel at a time in order to determine the position of the centre of each slit by reading the output from each individual pixel with a precision of 1% per pixel according to the diagram. Net light is not mentioned, and the system as described, has no need for it, nor should it be affected by it.
Another side note, on fig. 1 the numbers 78 and 79 are not the numbers represented by the binary sequences just below them.
Cheers.
Hello Bill,
Here is the residuals from 0-360* with a function of sin(8*A+40)*3.1" removed. The standard deviation of residuals after applying the function is 2.0". The sine wave may not be peaky enough when plotted so adding a second sine function with a shorter period should be better if it can add constructively to sharpen the peaks. I might look at that tonight. It may only be a minor effect.
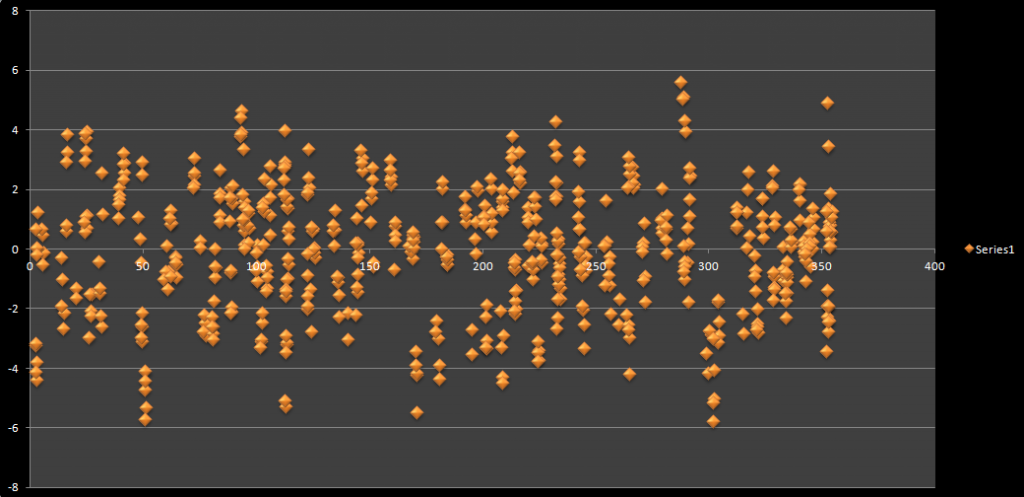
The removal of the instrument and rotating the studs should not affect the real-world work I usually do, but it may prove a disturbance at short ranges, where I do my testing. As I stated in the previous thread my experiments are certainly not perfect, and slightly longer ranges would probably be good for the results. I think I got what I wanted out of the angular experiments which was to practically assess what the total station might and might not be capable of in the bigger world. It seems it definitely debunks my earlier held belief that it was capable of near 1" like performance in a horizontal plane, and for that I'm better off.
Cheers.
> Not that it would affect the discussion much, but wide gaps are zeroes and thin are ones which means more light the more zeroes.
>
> That paragraph you posted mentions the array being read with a multiplexer. A multiplexer allows for fetching and single line (pixel) to send as output. From Wikipedia:
>
> >An electronic multiplexer makes it possible for several signals to share one device or resource, for example one A/D converter or one communication line, instead of having one device per input signal.
>
> It's job seems to be fetch from each individual pixel at a time in order to determine the position of the centre of each slit by reading the output from each individual pixel with a precision of 1% per pixel according to the diagram. Net light is not mentioned, and the system as described, has no need for it, nor should it be affected by it.
But all of the drawings of the circle reading system that I've seen published show the light source shining through the graduated circle to mirrors under the circle for reflection back through the circle to the CCD pixels. If that is in fact so, it means that the circle graduations, the net width of the transparent gaps forming zeroes and ones, consitute a variable screen that slightly dims the light transmitted through the first pass of the circle after leaving the source. The obscuring effect of that screen would show a course pattern of modulation with a period of 45 degrees as Bill's graph shows.
If the CCD is making the fine interpolation of the angle read by the light level received by the fractionally illuminated pixels, it isn't clear to me why a change in the net light level wouldn't be misread as a greater or smaller part of the pixel being illuminated, i.e. a small error in the fine reading calculated from the CCD readings.
This artifact of the system wouldn't likely exist if the optical path of the light didn't pass through the graduated circle twice. It may well be that the published diagrams are just incorrect or it may be how the dithering of the circle reading is built into the instrument to be overcome by software corrections.
I'll be quite surprised if the light passes through the circle twice. I think the diagram isn't clear enough. I'm guessing it's a packaging thing, and two tiny mirrors are a way to have all the rest of the componentry above the circle. As soon as you try to have components below the circle you now have to start passing the angle reader's data back and forth through a slip-ring which is, at the moment, only used for external power and older style comms output to data cables.



