Math Teacher there are at least 3 ways to calculate the mark to mark distance from old NAD 27 coordinates.
I used one of the other ways and am 1mm different from you so we have a good check.
JOHN NOLTON
MathTeacher, post: 455179, member: 7674 wrote: Fascinating concept. The sea level distance, 35,373.21 meters, is the ellipsoidal distance on the Clarke 1866 ellipsoid. This can be duplicated by INVERSE in the NGS Tool Kit. INVERSE3D uses the GRS80 ellipsoid exclusively, so getting a mark-to-mark distance from the NAD27 coordinates requires calculating the x,y, and z coordinates for both points. I got 35,385.543 meters for that distance, one centimeter different from the old published value.
Using the NAD86 (1992) coordinates and the GRS80 ellipsoid gives a mark-to-mark distance of 35,386.452 meters.
Ellipsoid height is problematic in both calculations. NAD27 assumed that the geoid and ellipsoid were the same (actually, close enough so that the difference is negligible), so orthometric heights are the same as ellipsoid heights. The data sheets for the two points do not give ellipsoid heights, so I calculated them as the sum of the orthometric and geoid heights, which may introduce some error.
The evidence seems to show a separation of almost an additional meter from 1922-23 to 1992.
Perhaps the section on reduction of distances in https://www.ngs.noaa.gov/PUBS_LIB/TMNOSNGS10.pdf Appendix I (starting on printed page 24; PDF page 30) might be useful...
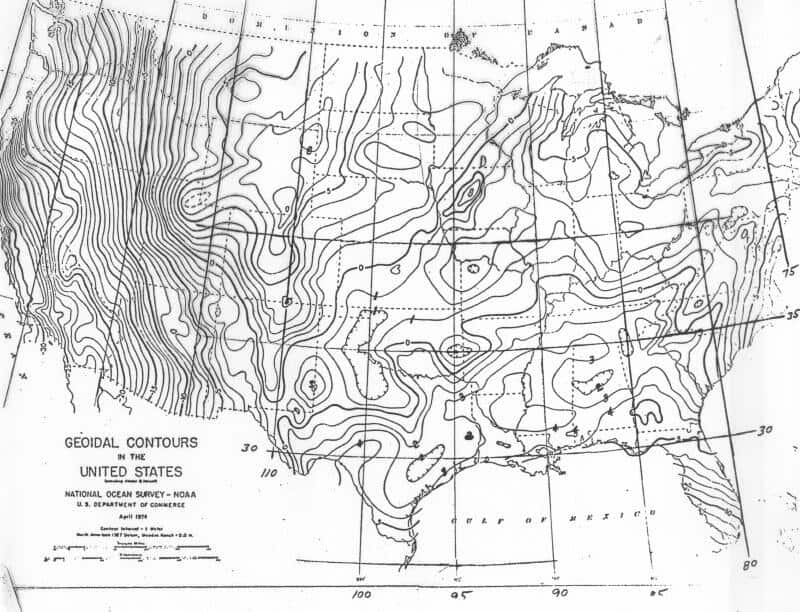
Actually, the reduction to the ellipsoid ("sea level") on NAD 27 in California was problematic....this map prepared in the 70's shows the bias present out there (6 m=1 ppm):
That is why, to me, mark-to-mark is the best format to use for representing (and archiving) distances. Unambiguous
See image file here: https://www.ngs.noaa.gov/GEOID/GEOID12B/GEOID12B_CONUS.shtml
To compare Mr Hamilton??s image.
I am using an iPad and cannot reduce image size in order to post it.
I agree with John in this case in regards to the straight line mark to mark distance being what I (and about 95 years ago, Dr. Michelson) want. That's the distance over which a light beam must travel. Reducing to ellipsoid height, while useful for some things, is fairly irrelevant here. Since the USCDG kindly supplied 35,385.53 meters, mark to mark, in 1923, I just need its modern equivalent. Unfortunately I haven't had time today to play with the transformation software.
Since a direct, mark to mark distance is what I'm after, would it make the most sense to use the X/Y/Z Cartesian coordinates for each BM and just compute the distance between them using simple trig?
Bill93, post: 455006, member: 87 wrote: Transform lat-lon-height coordinates to XYZ (HTDP can do that along with the other work) and do a 3-dimensional Pythagorean hypotenuse for the path distance.
Thought I heard it somewhere. I'm slow, but eventually catch on......
As [USER=640]@John Hamilton[/USER] posted, mark-to-mark is the best way to archive distances. As [USER=225]@JOHN NOLTON[/USER] said, there are several ways to compute mark-to-mark distances. Both points are well illustrated by the mark-to-mark computations on the NAD27 coordinates.
Determining the z-coordinates for calculating a mark-to-mark distance requires ellipsoidal height when the NGS INVERSE3D methodology is used. Thus, that parameter is relevant if the goal is to calculate distances as opposed to measuring them.
For determining movement of the two monuments relative to each other, no coordinate transformation is needed. Determining the individual movements of the monuments would require a coordinate transformation.
You can reduce an observed distance (slant range, instrument to prism) to mark to mark using either zenith distances (vertical angles) or delta heights (ellipsoidal). You can use delta orthometric heights along with geoid heights. Of course HI and HT are also required.
It is important that you are aware that distances on the ellipsoid or Geoid are arc distance measurements.
But, a GPS vector from XYZ to xyz is a chord measurement.
Paul in PA
Arc to chord corrections can be applied, but they are only significant over long distances. I don't remember the cutoff (currently out of the office), but it has the distance cubed in the denominator, if I recall correctly.
The EDM distance follows a curved path as well, which is NOT the same curved path as the optical observation for vertical angle. As above, the difference is very small, but it can be a factor over long distances.
For a really good discussion of ll of these issues, see Rueger...
Interesting history and discussion! but I'm left wondering .... why?
John Hamilton, post: 455262, member: 640 wrote: Arc to chord corrections can be applied, but they are only significant over long distances. I don't remember the cutoff (currently out of the office), but it has the distance cubed in the denominator, if I recall correctly.
The EDM distance follows a curved path as well, which is NOT the same curved path as the optical observation for vertical angle. As above, the difference is very small, but it can be a factor over long distances.
For a really good discussion of ll of these issues, see Rueger...
A typical baseline of 35 miles (30' of arc) needs to be corrected by 1/60,000.
For a 70 mile baseline (1?ø of arc) the correction is 1/14000. That is well within the range of typical concern.
Paul in PA
Andy J, post: 455263, member: 44 wrote: Interesting history and discussion! but I'm left wondering .... why?
Curiosity.
Mark to Mark distance has been known to be the best way to keep records of distance for a long time.
Mr. Vincenty and I had verbal conversations on this in mid 70's. He communicated this fact to G. Bomford
in 1978 ( see Geodesy by G. Bomford, 1980 4th edition, pg. 85).
One must also remember that a geoid map done in 1974 has NO bearing on work done in 1922-24.
Reduction done in 1922 was to sea level (no geoid undulation was used because they did not know it).
Also NAD27 and NAVD29 were not yet used.
JOHN NOLTON
JOHN NOLTON, post: 455285, member: 225 wrote: Mark to Mark distance has been known to be the best way to keep records of distance for a long time.
Mr. Vincenty and I had verbal conversations on this in mid 70's. He communicated this fact to G. Bomford
in 1978 ( see Geodesy by G. Bomford, 1980 4th edition, pg. 85).One must also remember that a geoid map done in 1974 has NO bearing on work done in 1922-24.
Reduction done in 1922 was to sea level (no geoid undulation was used because they did not know it).
Also NAD27 and NAVD29 were not yet used.JOHN NOLTON
i believe it has something to do with it...it shows the potential bias due to ignoring the geoid, which, as you state, they did not have sufficient knowledge of to use. So if they used sea level heights to reduce to the ellipsoid, then their reduced distance will be in error by several PPM. Of course, to compare slant range to slant range (i.e. to try to compute the speed of light), this is an unnecessary step.
Since we've been discussing this subject the past few days, I thought I'd share an article that was just published this evening in the San Bernardino Sun newspaper on MIchelson's speed of light experiment. The reporter actually spends some time describing the survey efforts made in support of the experiment.
This post is for 2 people; 1. OtherHand and 2. John Hamilton
1. OtherHand thanks for posting everything on this and for your last post above from the Sun newspaper.
2. John Hamilton from what I can find looking over the field notes on this job (survey in 1922-24) they did not reduce
to sea level to get the mark to mark distance that Dr. A.A. Michelson wanted. But they did reduce to sea level
to get the Lat., Long. USC&GS (now NGS) does keep all records of data reduced to the ellipsoid as you know.
The two forms used are, 1. Form 589, COMPUTATION OF ......................... BASE LINE was a field form. NO sea level reduction was made on this form. (here the blank space you fill in the name of the base line).
2. Form No. 543 BASE-LINE COMPUTATIONS was an office form and I see no reduction there but I do not have
all the office computations.
Please note that the forms listed I use the spelling as it IS on the forms.
JOHN NOLTOM
Well, I think I have my results, but never having used HTDP before I'm not 100% certain.
I started with my GPS observations at the Antonio BM (EV3805) from last month and returned by OPUS-Share using precise (final) orbital data. For the X/Y/Z values it gave -2452098.219/-4675488.645/3570415.759. The reference frame and epoch listed by OPUS as part of the result was NAD83 (2011) and epoch 2010.0000
Using HTDP, I input the data from the Michelson (EW1861) data sheet. It was listed as NAD83 (1992) with an epoch of 1991.35. For the reference frames input and output in HTDP I used NAD83, Pacific Tectonic Plate fixed. I input the 1992 coord values and set HTDP to bring them from 1991.35 to 2010.0000. I assume that even though it's 2010, it's considered "present"?
I obtained the following X/Y/Z coords for the Michelson BM after the transformation: -2483903.742/-4660191.420/3567857.906.
Computing the Pythagorean distance between my GPS coords for Antonio and the transformed Michelson station coords I obtained 35385.576 meters. This would be the present BM chord length or the line-of-sight distance between the two bench marks.
The 1923 survey data produced a result for that distance of 35,385.53 meters. Subtracting the two I get an increase in distance of 4.6 centimeters.
Does it appear I've done this correctly? Given inherent measurement errors and the possibility of mountain shift over 95 years, it seems like it's in the ballpark of what I'd expect to see (both BMs being on the west side of the San Andreas fault and on the same Pacific tectonic plate). My uncertainty stems from the fact OPUS gave me an epoch of 2010.0000 for observations I did last month.