Occaisionally, I have the 'opportunity' to explain these standards to other surveyors. I often ask other surveyors what their "confidence level" is in their results. The answer of "110 %" is guaranteed to elicit giggles.
There are some pretty common misconceptions involving the expected precision of an angle turning. Even I misunderstood some of the concepts, so I have tried to condense and codify what I think I know.
It is quite a few years since I have had the chance to read the DIN specs and I have only briefly had an encounter with the new ISO specs.
Terminology is quite important in the specs and is not interchangeable; one of the commonest errors made in these discussions.
Hopefully, I will get this right...
A pointing is one sighting of one target. Two pointings, one at the BS and one at the FS is a direction. Two directions, one in each face, is an angle. Two angles is a set or one repetition.
The DIN 18723 spec is not the accuracy of an angle. It is the uncertainty in pointing face direct and pointing face reverse at one target. This standard deviation is merely an expression of precision.
In order to apply the DIN spec to an angle one has to multiply the standard deviation by 2 then divide by the square root of the number of directions.
One must also remember that these results represent the standard deviation of 68 % confidence. In order to estimate the values of 95 % or 99.9 % confidence the appropriate multipliers are required.
These values then equate to optimal procedures, equipment and conditions. Poor pointing techniques, weak tripods, and sun shimmer quickly degrade results. For example, pointing to the apparent prism center rather than a manufacturer provided target can cause “prism confusion”, where the center of the apparent prism is, in effect, a mirage, displaced due to poor alignment of the prism to the instrument. Only after systematic biases are understood and compensated for might possibly standard deviation be a representation of accuracy.
The new ISO 12857 Part 2 standard created a new means of determining Theodolite accuracy. A test series of 5 targets spaced around the horizon evenly at distances from 100 to 250 meters are observed in four series of observations. Each observation comprises three sets of directions to each target. A least squares adjustment then determines the experimental standard deviation of a direction observed in both faces.
This standard has been revised and replaced by ISO 17123-3:2001 (which I have not had the pleasure to view).
In order to keep all this straight I made an excel sheet;
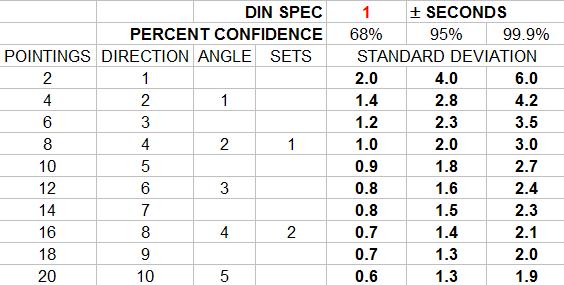
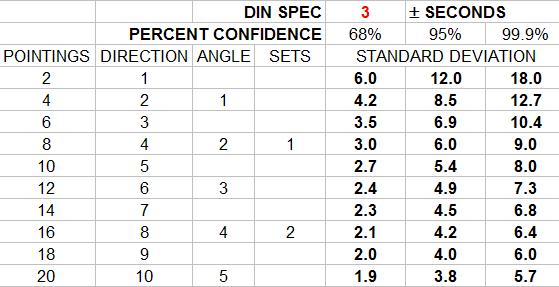
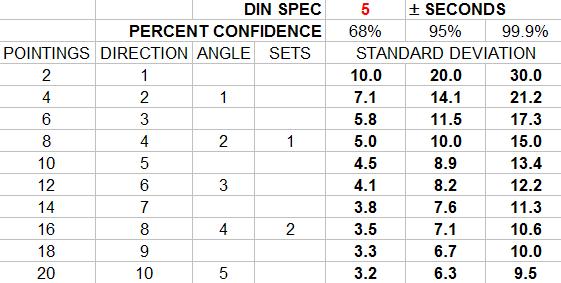
I have made an honest attempt at correctness here, so, of course, if somehow I have misspoken I am assured someone will kindly correct me.
One note, the math is done by the excel sheet, so...
Definition of "set"
Well, I can tell you that I use the word "set" somewhat differently than you have above. I had, in fact, to this moment considered Bomford's usage to be definitive, namely:
A pointing comprises a single intersection of an object and the reading of the circle.
A measure of an angle or direction is obtained by subtracting the circle reading of one object from that of another. Such readings may involve the mean of several pointings.
A set is a pair of measures, FL and FR.
(The above is taken from the 3rd Edition of G. Bomford's "Geodesy".)
Is there some other usage of "set" in the surveying literature?
Kent, in Referring To An Angle Per DIN Specs
One accepts the DIN definition.
A pointing comprises a single intersection of an object and the reading of the circle.
An observation of an angle or direction is obtained by subtracting the circle reading of one object from that of another
A measure of an angle or direction is obtained by meaning a pair of observations, D & R.
A set is a pair of measures, 2D and 2R.
It appears you happily ignore the equivocation in your quote:
"Such readings may involve the mean of several pointings".
Because in "mensuration" such readings do involve the mean of several sets of observation, 2, 3 or more depending on the final requirements and the inherent precision of the available observing instrument.
DIN specs allow one to anticipate the precision of a set of 2D & 2R assuming no error in the pointing which was the case in a DIN factory test because the pointings were made through a collimator and were effectively at infinity.
The new ISO test while provides a comparable value between instruments under the same test but is in no way comparable to a DIN test.
Paul in PA
Definition of "set"
Your definition makes sense if turning multiple sets or using an old vernier style (T2) theodolite, as the initial reading on the backsight would be something other than 0°.
I've always considered a set as BSD, FSD, FSR, BSR.
P.L. ?
Does not matter if backsight direct is zero or any other number.
Paul in PA
Bomford was English.
DIN is German.
Wouldn't be the first difference of opinion between those particular nationalities.
Bomford was English.
> DIN is German.
> Wouldn't be the first difference of opinion between those particular nationalities.
Well, you posted in English, didn't you? If you have a copy of the "Handbuch der Vermessungskunde" perhaps you can quote the German definition it gives. That would be interesting.
P.L. ?
True, but the example given by Kent refers to what is recorded. With today's instruments, it is a touch of a button to zero up, and if it drifts a second or two, nobody gets too bent out of shape.
I'm sure you've kept notes where you recorded the backsight observation, as in your example you spell out subtracting the foresight observed angle from the backsight observed angle. For the time when the text was written, an assumed zero on the backsight was not an option.
Kent, in Referring To An Angle Per DIN Specs
> One accepts the DIN definition.
>
> A pointing comprises a single intersection of an object and the reading of the circle.
>
> An observation of an angle or direction is obtained by subtracting the circle reading of one object from that of another
>
> A measure of an angle or direction is obtained by meaning a pair of observations, D & R.
>
> A set is a pair of measures, 2D and 2R.
>
> It appears you happily ignore the equivocation in your quote:
>
> "Such readings may involve the mean of several pointings".
No, not really. Bomford is very straightforward. In measuring angles by observing sets of direction angles over distances common in the triangulation nets of classical geodesy, it wasn't unreasonable to make several pointings on a target before changing face. That merely demonstrated that the pointing was apparently blunder free. It would have been more common practice under suboptimal conditions, less so otherwise.
P.L. ?
> True, but the example given by Kent refers to what is recorded. With today's instruments, it is a touch of a button to zero up, and if it drifts a second or two, nobody gets too bent out of shape.
No, under the common usage that Bomford gives, one can speak of sets of directions and sets of angles. The word "set" means simply that pairs on opposite faces of the instrument are observed in order to cancel collimation errors.
Scott
Why do you use empirical values instead of the actual values for the confidence intervals? We are talking about precision right?
excellent post....thank you Scott, Kent .....et.al
Jordan?
Kent, if you have it handy, it might be interesting.
Ramsayer und Mueller
Here is the next best thing to finding the definition (in German) given by the "Handbuch der Vermessungskunde". It's from the 1978 text entitled "Introduction to Surveying" (Frederick Ungar, NY) written by Ivan Mueller and by Karl Ramsayer, one of the authors of one of the volumes of the German handbook mentioned.
Per Ramsayer and Mueller:
The periodic errors of the graduation are eliminated by observing the angle in n sets (one set = one measurement of the angle in two faces) where for each set the horizontal circle is shifted by 180°/n.
This is, of course, essentially the same sense in which Brigadier Bomford uses the word "set".
Bomford was English.
Yes, and so is the German in which the text explains that Band I deals with the theory of errors and least squares estimation.
Where one is looking for the meaning of the word "set" as used in surveying, he or she is pretty much stuck with English and German, which is why Mueller and Ramsayer's text is so useful. They are German speakers writing in English about surveying topics including what a "set" is. :>
Maybe this is covered in the spec, but it isn't at all clear to me.
If the published spec is for one pointing, then for 2 pointing isn't the std dev = sqrt(2)*spec? For two values with random error, their difference should have twice the variance and therefore 1.414 times the std dev.
The result would always be just sqrt(Pointings)*spec ?
> If the published spec is for one pointing,
Actually, the DIN spec is for the standard error of a direction taken as the mean of two pointings on opposite faces, just as one would expect. So, yes, the standard error of an angle taken as a set is
s [SQRT(2)]
Where s is the standard error of a direction taken as the mean of FL and FR pointings.
Kent ?
Whether or not several pointing were done before changing face is irrelavent to the mathematics.
But it still takes a set with a minimum of 2D & 2R in order to turn an angle within the DIN 18627 specs for an instrument.
Paul in PA
Kent ?
> But it still takes a set with a minimum of 2D & 2R in order to turn an angle within the DIN 18627 specs for an instrument.
If by "2D & 2R" you mean an angle obtained by subtracting two directions, each taken as the mean of FL and FR pointings, you're right. I understood you to be arguing for something else in your post above, however. A set is the mean of two measures, one taken FL and one FR.



