This is from the XKCD website.?ÿ I think many people on this board will like it.
?ÿ
Excellent!
I think the movie was called Brewster's Millions starring Richard Pryor.?ÿ He worked for some big company in an office that involved paying employees.?ÿ He realized that applying certain percentages to pay earned (social security, etc.) resulted in numbers like $453.125 or $764.334.?ÿ He found a way to slide those fractions of a cent over into a hidden account for him.
I may be off on exactly what he did, but the result was the same.?ÿ He was rich and nobody knew it.
Excellent!
I think the movie was called Brewster's Millions starring Richard Pryor.?ÿ He worked for some big company in an office that involved paying employees.?ÿ He realized that applying certain percentages to pay earned (social security, etc.) resulted in numbers like $453.125 or $764.334.?ÿ He found a way to slide those fractions of a cent over into a hidden account for him.
I may be off on exactly what he did, but the result was the same.?ÿ He was rich and nobody knew it.
superman 3
This is from the XKCD website.?ÿ I think many people on this board will like it.
?ÿ
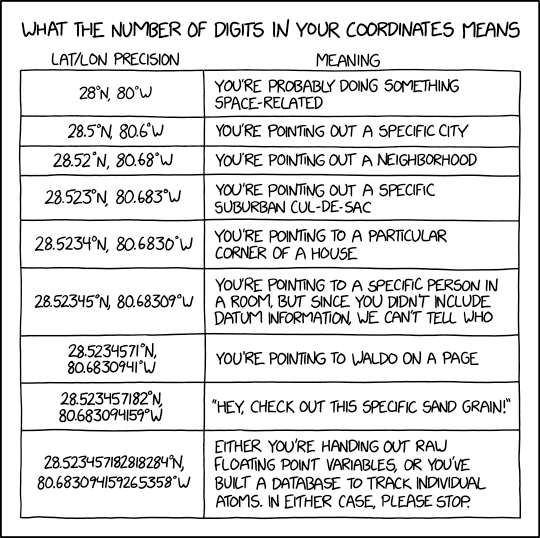
We learned that we had to carry out to the 9th place in Geodesy with your calcs because ignoring those decimals in your calculations would result in errors when working with inversing over 100's of kilometers.
Also, taking a coordinate in meters and converting it to feet in the US meant you needed to go out past a certain decimal or you would be at least 1.5 feet off of your original coordinate in NJ. 3937/1200 is the standard. Use it. Love it. At least until 2022
?ÿ
You are correct.
Richard Pryor was in both movies, though. Thanks for correcting my feeble movie memory.
Also Office Space. Milton lost his Swingline but burned down the building and left with the check.
Well, son of a gun. Same basic plan. I never watched that movie, though.
A quirk in the latitude, longitude system and the circumference of the earth means there is 100' of distance between a second of arc in latitude. Approximately.?ÿ
So one second of arc is 100', 0.1"=10', 0.01"=1'.
Beyond 4 places, what are you doing?
Of course for longitude that only works near the equator. At my general area I figure a second of longitude =70' plus or minus.
Just a way to think of distance between latitude longitude coordinates without calculating. I've never got a feel for decimal degrees, I just know most regulators want 5 places.?ÿ
Hmmm. If I inverse between NGS marks KV5560 in Trenton, NJ and AD9364 in San Diego CA, I get 3,853,254.4307 meters, or 3,853.2544307 km. If I move KV5560 northeast by adding 0.00001 to its latitude and subtracting 0.00001 from its longitude and then move AD9364 southwest by an analogous operation, the distance changes to 3,853,254.4313 meters or 3,853.2544313km.?ÿ
The difference is 0.6 millimeter. It's hard to see how adding decimal places to either station's coordinates would improve the distance calculation.
No, I think that the third decimal place is millimeters so the fourth would be tenths of a millimeter.
I agree, but the change is in the third place so 6mm or .6cm, however, I'm a non-metric kinda guy so maybe I'm missing something.
xxx.4313 - xxx.4307 = 0.0006 meter = 0.06 cm = 0.6 mm
In Dave Lindell post the cartoon id using Degrees and decimal of a degree.
In your NGS inverse you are using Degrees minutes and seconds plus decimal of a second.
It looks like most posters here are getting confused between the two?
I would like to point out that 0.00001 second of arc is around 0.2mm.
The inverse program that NGS uses is Vencinty's and only good to around 0.15 mm.
There are other inverse programs that can do better.
JOHN NOLTON
If you spend a little time with Bowditch, you may abandon state plane forever.
On the other hand, if you're talking about decimal degrees, that makes perfect sense. The proportion 1/10^n = x/3600 can be used to determine how many seconds are represented by an n-decimal place degree. For example, 1/10^3 = 0.001 degree.?ÿ
As @steven-metelsky says, you have to use 9 decimal places to get similar accuracy to 5 decimal places in seconds.
?ÿ
Yeah, dang it, I didn't look closely enough at the table. My reply to my own post above may help reconcile the difference.
Thanks for correcting my error.







