In the January 2017 issue of The American Surveyor, the Test Yourself problem solution by the author, Dave Lindell, used a geometric construction. I solved it by applying trigonometry.
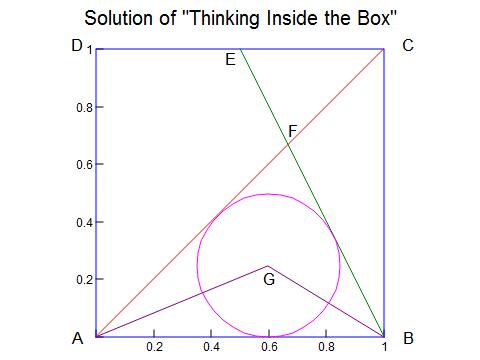
Solution of "Thinking Inside the Box"
====================================
This solution is based on the fact that the center of a circle inscribed
in a triangle is at the intersection of the bisector of the vertex angles
The square is assumed to be a Unit Square (side = 1)
<EBC: 26.5651 [tan(0.5/1)]
<CEB: 63.4349 [tan(1/0.5)]
<ABC: 90.0000
<BAG: 22.5000 [<BAC / 2]
<ABG: 31.7175 [<CEB / 2]
<AGB: 125.7825 [180 - <bac + <ABG]
AG: 0.648057 [1 * sin(<ABG) / sin(<AGB)]
Radius: 0.248001 [AG * sin(<BAG)]
Here's the link to the published problem: http://www.amerisurv.com/PDF/TheAmericanSurveyor_Lindell-TestYourself38_January2017.pdf
Link to Dave Lindell's solution: http://www.amerisurv.com/PDF/Lindell_Test%20Yourself38_ThinkingInsideTheBox_Solution.pdf
I have enough problems, to pass on these brain teasers!
(Go for it, the rest of ya!)
Very Nice; BUT
1. there is always the problem of just how many digits to carry with a solution like yours (I myself use 10).
2. Dave has never said that his solutions to the problems he post are the only solutions and that they are the best solution or shortest.
I like Dave's equation for r , r = 2*s/ (3+ 2*sqrt 2 + sqrt 5) and leave it in that form. Its more pure to me. (s = the side of the square)
JOHN NOLTON, post: 420014, member: 225 wrote: Very Nice; BUT
1. there is always the problem of just how many digits to carry with a solution like yours (I myself use 10).
2. Dave has never said that his solutions to the problems he post are the only solutions and that they are the best solution or shortest.I like Dave's equation for r , r = 2*s/ (3+ 2*sqrt 2 + sqrt 5) and leave it in that form. Its more pure to me. (s = the side of the square)
With respect to digits: my calculations were done in the J Programming language (www.jsoftware.com) using double precision numbers with about 16 digits of precision. The J script used follows:
NB.%inside-box.ijs - caption
NB. Modified: 2017-03-23
NB. Solution of 'Thinking Inside the Box' by Dave Lindell.
NB. The American Surveyor January 2017
NB. http://www.amerisurv.com/PDF/TheAmericanSurveyor_Lindell-TestYourself38_January2017.pdf
NB. =========================================================
r2d=:180*1p_1*]
o=: smoutput
arctan=: _3&o.
sin=: 1&o.
fd=: 13 : ('10j4": r2d y'),
title=: 'Solution of "Thinking Inside the Box"'
o LF, title,LF,(#title)#'='
o 'This solution is based on the fact that the center of a circle inscribed'
o 'in a triangle is at the intersection of the bisector of the vertex angles'
o 'The square is assumed to be a Unit Square (side = 1)'
ebc=: arctan 0.5%1
ceb=: arctan 1%0.5
o ''
o '<EBC: ',(fd ebc),' [tan(0.5/1)]'
o '<CEB: ',(fd ceb),' [tan(1/0.5)]'
o '<ABC: ',fd ebc+ceb
o ''
bag=: -:arctan 1
abg=: -:ceb
agb=: 1p1-bag+abg
o '<BAG: ',(fd bag),' [<BAC / 2]'
o '<ABG: ',(fd abg),' [<CEB / 2]'
o '<AGB: ',(fd agb),' [180 - <bac + <ABG]'
o ''
ag=: 1*(sin abg)% sin agb
o 'AG: ',(12j6":ag),' [1 * sin(<ABG) / sin(<AGB)]'
r=: ag*1&o.bag
o 'Radius:',(12j6":r),' [AG * sin(<BAG)]'
NB. create a plot
require 'plot'
pd 'reset'
pd 'aspect 1'
pd 'grids 0 0; frame 0'
pd 'title ',title
pd 'type line'
pd 0j0 0j1 1j1 1j0 0j0
pd 0j0 1j1
pd 1j0 0.5j1
pd 0j0, (ag r. bag ),1j0
pd (ag r. bag)+ r r. ((i.36)*2p1%36),0
pd 'textc 160 85 A'
pd 'textc 850 85 B'
pd 'textc 850 900 C'
pd 'textc 160 900 D'
pd 'textc 480 860 E'
pd 'textc 610 660 F'
pd 'textc 560 250 G'
pd 'show'
pd 'save jpg "C:UsersTom ArnesonSkyDrivej64-805-userSurveyProblemstestyourself-box"'
Note 'output'
Solution of "Thinking Insde the Box"
====================================
This solution is based on the fact that the center of a circle inscribed
in a triangle is at the intersection of the bisector of the vertex angles
The square is assumed to be a Unit Square (side = 1)
<EBC: 26.5651 [tan(0.5/1)]
<CEB: 63.4349 [tan(1/0.5)]
<ABC: 90.0000
<BAG: 22.5000 [<BAC / 2]
<ABG: 31.7175 [<CEB / 2]
<AGB: 125.7825 [180 - <bac + <ABG]
AG: 0.648057 [1 * sin(<ABG) / sin(<AGB)]
Radius: 0.248001 [AG * sin(<BAG)]
)
tomarneson, Thanks for the information above about jsoftware and the link to it. Again it is a very nice solution you have.
JOHN NOLTON