nm
Very tricky. The COGO guys are going to be very frustrated by an apparent lack of information, but it seems to be solvable anyway.
40
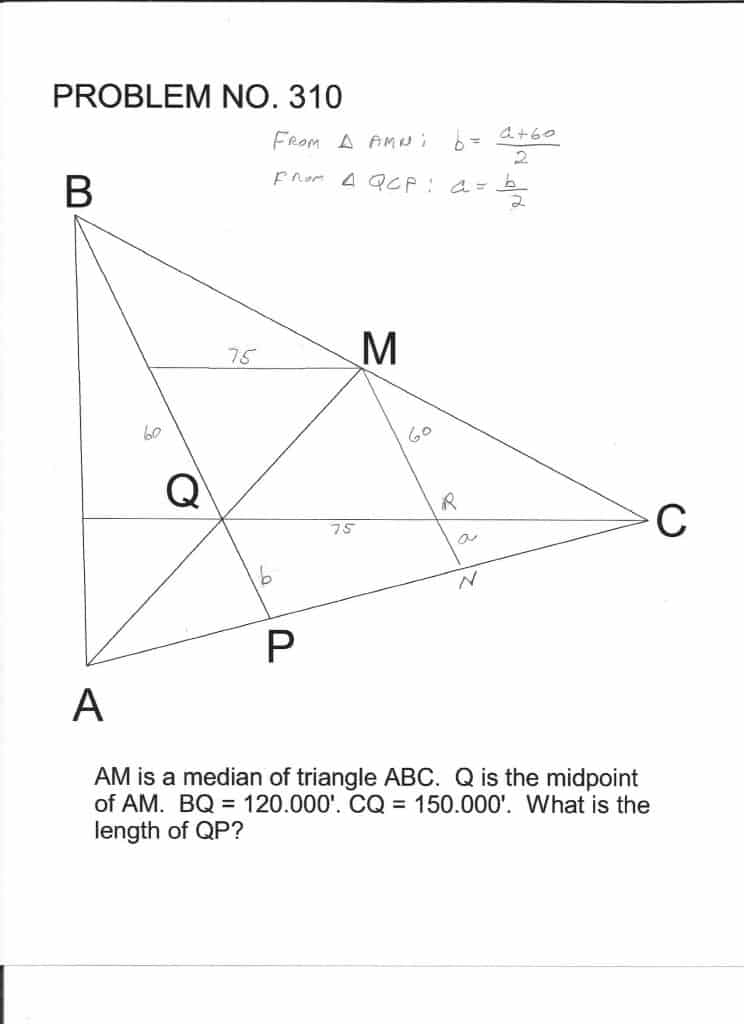
Very easy to solve with cogo. Draw two concentric circles, one with a radius of 120 and the other with a radius of 150, the center is point Q. Draw a line from the center to a random point on the 120 radius circle (this is point B) and another line from the center to the 150 radius circle (this is point C). Connect the endpoints of these lines (this is line BC). Find the midpoint of line BC (this is point M), now draw MQ and create a circle centered on Q with radius QM. Extend line MQ to the far side of circle with radius QM, (this intersection is point A). Draw line AC and intersect with line BQ to create point P. Inverse QP and find that the answer is always 40 regardless of the shape of ABC.
Yep, the answer is 40.
Dave Lindell, post: 324895, member: 55 wrote: Yep, the answer is 40.
Did they let you use a cogo calculator in the exam? Stephen's solution is logical using a cogo calculator, but the computation of the unknown line without a cogo calculator requires the use of the law of sines and the law of cosines, and a geometric and conclusion based upon the data given.
I used triangle BCQ and realized that any distance you want for line BC that is less than 270 meets the data given. I just assumed 200 for line BC. Could have been done by applying a constant instead of 200, but during a test the use of real numbers seems simpler to me. Medial line AM, by definition, intercepts the midpoint of BC. So BM=MC=100. That gives us all three sides of triangle BCQ. From there, several steps using law of sines and law of cosines are required to eventually reach the answer.
If they let you use a cogo calculator on this test, the problem is fairly quickly solved if one knows that medial line bisects the side and that the 120 and 150 set a direction for line MA, regardless of the length of bc, subject to the limit of 270.
If they did not let you use cogo calculator, it is my opinion that this problem is not a fair problem if this is a timed test with a lot of questions on it. The random circles and inverse, etc that Stephen used are not quickly solved by hand.
Is the test multiple choice? If so, I'd have quickly scaled the length of the unknown line.
OK, Mister Geometry Teacher, it has been 10 days now. We all agree the answer is 40. We are ready for your lecture as to the various theorems, postulates and corollaries that apply which dictate the answer will be four-twelfths of the first number and four-fifteenths of the second number. Probably some connection to the old 3-4-5 triangle based on the twelfths and fifteenths involved.
Holy Cow, post: 325858, member: 50 wrote: OK, Mister Geometry Teacher, it has been 10 days now. We all agree the answer is 40. We are ready for your lecture as to the various theorems, postulates and corollaries that apply which dictate the answer will be four-twelfths of the first number and four-fifteenths of the second number. Probably some connection to the old 3-4-5 triangle based on the twelfths and fifteenths involved.
Is that question for me?
The solution is shown above.
Oops! Missed the attached pdf with the solution.
I think a few more steps in the answer would help. Certain equalities are presented that require explanation. Sort of a geometry refresher lesson. Certain things aren't as intuitively obvious today as they were back in the days when we actually had to think about things instead of turning it all over to the "black box" and software. My rust is showing.
Draw a segment from M to BQ parallel to QC. That segment will be 75. Draw a segment from M parallel to BQ. That segment will be 60. Both of these are true because similar triangles are created by the constructed segments.
Extend the segment parallel to BQ until it meets AC. Call that point N. Then QP will be half of segment MN. Call the intersection of MN with QC point R. Then RN will be half of QP.
Let a = RN, b =QP, and, since MR = 60, a = b/2 and b = (60 + a)/2. Solving, a = 20 and b = 40.
Wait! Not all of the rust is gone yet.
"Then QP will be half of segment MN."
Why do we know that to be true?
Look at triangle AMN. QP bisects AM and is parallel to MN (by construction). That makes triangle AQP similar to triangle AMN. Since AQ is half of AM (given), QP is half of MN.
To get a = b/2, follow the same reasoning with triangles QPC and RNC.
Dave didn't know this, but he's greatly responsible for my interest in surveying mathematics and geodesy. Sometime around 2003-04, I did an internet search for geometry problems. One of his problems from Professional Surveyor came up. I subscribed to the magazine to get his problems, but found a whole 'nother world between those pages.
I've used his problems everywhere from Introduction to Geometry to Calculus II. He gave me a rich supplemental source for teaching mathematics.
Thanks, Dave!
I am missing something. How are you getting 75?
Senility! We all need a bit more.
I totally forgot the part about AQ = QM. That makes a big difference.
Segment M(Unnamed Point) is 75 because each side of triangle B(Unnamed Point)M is one half of its corresponding side in triangle BQC. The construction of segment M(Unnamed Point) parallel to QC guarantees this. QR is 75 because QRM(Unnamed Point) is a parallelogram whose opposite sides are equal.
Here's a secondary question: Will BQ always be 3/4 of BP regardless of the given lengths?
This is a great problem for several reasons, but, in modern educational jargon, its solution demands "critical thinking." Math and science teachers have been amused at "educators" discovering the thinking processes they've been using and teaching for centuries.
Heck, you guys are among the best of all critical thinkers in the world, so you know what I'm talking about.
A major weakness in today's math instruction is that it is imperative to write down every step in the solution process no matter how tiny. Then they dish out 45 nearly identical problems demanding all of this jabberwocky every time.
Math people can jump several steps at a time because they "know" what they are doing. That is no longer deemed to be acceptable. Brilliance be damned.
Every math problem is to be broken into a minimum of four steps. And the student must be able to describe each step, not just do it. So the student spends hours on meaningless foolishness and is allowed no time to explore higher level challenges.
It's frustrating for everyone involved. At the middle school level and below, that sort of carrying on is "critical thinking." As you pointed out, it's really just administrative overhead. At the high school level, we required a certain amount of shown work to discourage cheating on tests and quizzes. Unsupported answers got no credit.
The way the Advanced Placement program grades free response math questions is a good way to do it. A question may be worth, say, 7 points. The answer will be maybe 2 points, and necessary intermediate answers will each have a point value. So, if the student gets all answers correct, he/she earns 7 points but can earn some points without completely solving the problem.
In Dave's problem, a student would have earned points for the parallel segment construction, the similar triangle analysis, and, finally, the correct answer. But, the CAD solution is valid in today's world and the education system has not figured out how to credit it. Some math teachers embrace technology and spend hours incorporating it while others ignore it and demand the kind of work you described. I was somewhere in the middle, primarily using technology to reinforce mathematics, but sometimes using it as an alternative route to laying out the mathematics.
My department head at the community college, on the other hand, gave no partial credit. His reasoning? With generous partial credit available, an engineering student could graduate without ever having successfully solved an engineering problem completely.
It would take more of the teacher's time, but I think the ideal grading system would give full credit for correct answers on the due date, and diminishing credit for correct answers later, but with the requirement that every problem had to be eventually gotten correct in order to pass the course.
Some of my colleagues did something like that. They would conduct test correction sessions. Students were required to solve missed problems correctly, explain their error, explain the correct solution, and then formulate and solve a similar problem. For this, they received 1/2 credit for the problem added to their original test score.
I, being a glutton for punishment, allowed retakes on some tests. Students were required to attend two 45-minute tutoring sessions either before school or after school, then take a ten-problem retest on the material. The higher of the original or retest grades was their final test grade. Answers were either right or wrong; no partial credit on the retest. The results were usually not good, but students were better-prepared for future tests. For me, it guaranteed a string of 12-hour days followed by a Sunday afternoon of grading papers.
For some general insight into how well retesting works, compare the pass rates for first-time takers and second-or-more-time takers of career exams like surveying exams, engineering exams, bar exams, etc. It's not pretty; the truth is that if you fail on the first try, you're even more likely to fail on the second one.